��Ŀ����
��ͼ����ƽ��ֱ������ϵxOy�У�AB��x���ϣ���ABΪֱ���İ��O����y�������ύ�ڵ�C������BC��AC��CD�ǰ��O�������ߣ�AD��CD�ڵ� D��
D��
��1����֤����CAD =��CAB��
��2����֪������ ��A��B��C���㣬AB=10 ��tan��CAD=
��A��B��C���㣬AB=10 ��tan��CAD= ��
��
�� �������ߵĽ���ʽ��
�� �ж������ߵĶ���E�Ƿ���ֱ��CD�ϣ���˵�����ɣ�
�� �����������Ƿ����һ��P��ʹ�ı���PBCA��ֱ�����Σ������ڣ�ֱ��д����P������(��д������)���������ڣ���˵�����ɣ�
�⣺
 |
(1)֤��������O'C,�� CD�ǡ�O�������� �� O'C��CD.
�� AD��CD,�� O'C‖AD,�� ��O��CA=��CAD
�� O��A=O'C, ���O��CA=��CAB �� ��CAD=��CAB
 (2)��AB��
(2)��AB�� ��O����ֱ�������ACB=90��.
��O����ֱ�������ACB=90��.
��OC��AB,���CAB=��OCB,��∆CAO��∆BCO�� ��OC²=OA∙ OB
��OC²=OA∙ OB
��tan��CAO=tan��CAD= , ��AO=2CO
, ��AO=2CO
�� ��AB=10,��OC²=2CO(10-2CO), ��CO>0 ��CO=4,AO=8,BO=2
��A(-8,0),B(2, 0),C(0,4) ..�� ������y=ax²+bx+c��A��B��C���㣬��c=4
0),C(0,4) ..�� ������y=ax²+bx+c��A��B��C���㣬��c=4
�� ���
���
‚��ֱ��DC��x���ڵ�F����∆AOC��∆ADC
�� AD=AO=8, ��O'C‖AD ��∆FO��C��∆FAD �� 
��8(BF+5)=5(BF+10), �� BF= , F(
, F( ,0)
,0)
��ֱ��DC�Ľ���ʽΪy=kx+m,�� ��
��
�� .
.
��
��E��-3�� ������ֱ��DC�Ľ���ʽ
������ֱ��DC�Ľ���ʽ ��
��
�ұ�=
�� �����߶���E��ֱ��CD�� .
ƒ����,

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д� ��һ�߳�Ϊ2a��b����һ�߳�Ϊa��b����ó����ε����Ϊ(����)��
��һ�߳�Ϊ2a��b����һ�߳�Ϊa��b����ó����ε����Ϊ(����)��



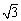 cmΪ�뾶��Բ���
cmΪ�뾶��Բ��� �ı����У���д��t��ȡ������ֵ ��
�ı����У���д��t��ȡ������ֵ ��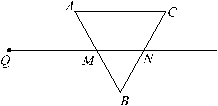
 ��ͼ����ͼ��ʾ������������ԭ��O��ת
��ͼ����ͼ��ʾ������������ԭ��O��ת ������ת��������ߵĽ���ʽΪ( )
������ת��������ߵĽ���ʽΪ( )  B��
B��
 D��
D��

