题目内容
射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,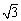 cm为半径的圆与△
cm为半径的圆与△ 的边相切,请写出t可取的所有值 .
的边相切,请写出t可取的所有值 .
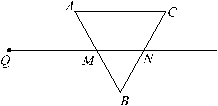 |
t=2或3≤t≤7或t=8

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
如图1,将两个完全相同的三角形纸片 和
和 重合放置,其中
重合放置,其中
 .
.
 | |||
 | |||
(1)操作发现
如图2,固定 ,使
,使 绕点
绕点 顺时针旋转.当点
顺时针旋转.当点 恰好落在
恰好落在 边上时,填空:
边上时,填空:
图1 图2
① 线段 与
与 的位置关系是 ;
的位置关系是 ;
② 设 的面积为
的面积为 ,
, 的面积为
的面积为 ,则
,则 与
与 的数量关系是 ,证明你的结论;
的数量关系是 ,证明你的结论;
(2)猜想论证
 当
当 绕点
绕点 旋转到图3所示的位置时,小明猜想(1)中
旋转到图3所示的位置时,小明猜想(1)中 与
与 的数量关系仍然成立,并尝试分别作出了
的数量关系仍然成立,并尝试分别作出了 和
和 中BC,CE边上的高,请你证明小明的猜想.
中BC,CE边上的高,请你证明小明的猜想.
 下列图象中,能表示
下列图象中,能表示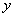 与
与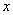 的函数关系的图象大致是
的函数关系的图象大致是

 过A、B、C三点,AB=10 ,tan∠CAD=
过A、B、C三点,AB=10 ,tan∠CAD= .
.
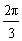 -
-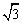 B.
B.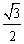 C.π-
C.π-
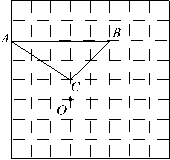 (1)如右图,已知△
(1)如右图,已知△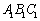 ,在网格中画出△
,在网格中画出△

 经过(0,-1),(3,2)两点.
经过(0,-1),(3,2)两点.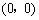 B.
B. C.
C.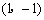 D.
D.
