题目内容
已知:如图,AB是⊙O的直径,⊙O过BC的中点D且DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠C=30°,CD=12,求⊙O的直径.
 |
证明: (1)联结OD.
 AB是直径,
AB是直径,
∴O是AB的中点.
 D是BC的中点,
D是BC的中点,
∴OD∥AC.
∴∠AED+∠EDO=180°.

 DE⊥AC,
DE⊥AC,
∴∠AED=90°.
∴∠EDO=90°.
 D是⊙O上一点,
D是⊙O上一点,
∴DE是⊙O的切线.
(2)联结AD.
 AB是⊙O的直径,
AB是⊙O的直径,
∴∠ADB=90°,
∴△ADC是直角三角形.
 ∠C=30°,CD=12,
∠C=30°,CD=12,
∴AD=CD·tan30°.
∴AD= .
.
 OD∥AC,
OD∥AC,
∴∠C=∠ODB=30°.
 OB=OD,
OB=OD,
∴∠B=∠ODB=30°.
∴∠AOD=60°.
∴OA=OD=AD= .
.
∴AB=


练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

 ,相似比为3:1,且
,相似比为3:1,且 的周长为18,则
的周长为18,则 的周长为 .
的周长为 .  的图象经过A、B两点,求出这个二次函数解析式.
的图象经过A、B两点,求出这个二次函数解析式.
 下列图象中,能表示
下列图象中,能表示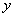 与
与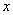 的函数关系的图象大致是
的函数关系的图象大致是

 过A、B、C三点,AB=10 ,tan∠CAD=
过A、B、C三点,AB=10 ,tan∠CAD= .
.
 经过(0,-1),(3,2)两点.
经过(0,-1),(3,2)两点.