题目内容
(1)如图1所示,△ACB和△ECD都是等腰三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于点F,试判断AE与BD的数量关系及位置关系,并证明你的结论.
(2)若△ECD绕顶点C顺时针转任意角度后得到图2,图1中的结论是否任然成立?请说明理由.
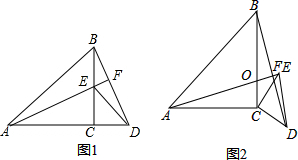
(2)若△ECD绕顶点C顺时针转任意角度后得到图2,图1中的结论是否任然成立?请说明理由.

考点:全等三角形的判定与性质
专题:
分析:(1)根据SAS推出△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠DBC,根据∠ACB=90°求出∠CAE+∠AEC=90°,求出∠DBC+∠BEF=90°,根据三角形内角和定理求出∠BFE=90°即可;
(2)根据SAS推出△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠DBC,根据∠ACB=90°求出∠CAE+∠AOC=90°,求出∠DBC+∠BOE=90°,根据三角形内角和定理求出∠BFO=90°即可.
(2)根据SAS推出△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠DBC,根据∠ACB=90°求出∠CAE+∠AOC=90°,求出∠DBC+∠BOE=90°,根据三角形内角和定理求出∠BFO=90°即可.
解答:(1)AE⊥BD.
证明:在△ACE和△BCD中
∴△ACE≌△BCD(SAS),
∴∠CAE=∠DBC,
∵∠ACB=90°,
∴∠CAE+∠AEC=90°,
∵∠CAE=∠DBC,∠AEC=∠BEF,
∴∠DBC+∠BEF=90°,
∴∠BFE=180°-90°=90°,
∴AE⊥BD;
(2)解:结论还成立,
理由是:∵∠ACB=∠ECD,
∴∠ACB+∠BCE=∠ECD+∠BCE,
即∠ACE=∠BCD,
在△ACE和△BCD中
∴△ACE≌△BCD(SAS),
∴∠CAE=∠DBC,
∵∠ACB=90°,
∴∠CAE+∠AOC=90°,
∵∠CAE=∠DBC,∠AOC=∠BOE,
∴∠DBC+∠BOE=90°,
∴∠BFO=180°-90°=90°,
∴AE⊥BD.
证明:在△ACE和△BCD中
|
∴△ACE≌△BCD(SAS),
∴∠CAE=∠DBC,
∵∠ACB=90°,
∴∠CAE+∠AEC=90°,
∵∠CAE=∠DBC,∠AEC=∠BEF,
∴∠DBC+∠BEF=90°,
∴∠BFE=180°-90°=90°,
∴AE⊥BD;
(2)解:结论还成立,
理由是:∵∠ACB=∠ECD,
∴∠ACB+∠BCE=∠ECD+∠BCE,
即∠ACE=∠BCD,
在△ACE和△BCD中
|
∴△ACE≌△BCD(SAS),
∴∠CAE=∠DBC,
∵∠ACB=90°,
∴∠CAE+∠AOC=90°,
∵∠CAE=∠DBC,∠AOC=∠BOE,
∴∠DBC+∠BOE=90°,
∴∠BFO=180°-90°=90°,
∴AE⊥BD.
点评:本题考查了全等三角形的性质和判定的应用,解此题的关键是推出△ACE≌△BCD,注意:全等三角形的对应边相等,对应角相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
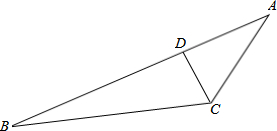 如图,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,则下列各式正确的是( )
如图,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,则下列各式正确的是( )| A、AD=BC-CA |
| B、AD=BC-CD |
| C、BD=AC+CD |
| D、AC=BD-AD |
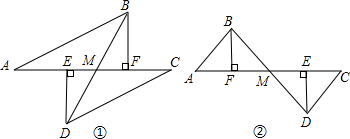
 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OA于D,G,交OB于点E,连接DE并延长DE交AB于F,且DE⊥AB
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OA于D,G,交OB于点E,连接DE并延长DE交AB于F,且DE⊥AB