题目内容
12.已知平行四边形ABCD的对角线AC=a,BD=b,且$\sqrt{a-6}$+|b-a+2|=0,下列哪个长度能作为平行四边形一条边的长度( )| A. | 3.5 | B. | 5.5 | C. | 7 | D. | 10 |
分析 首先由算术平方根和绝对值的非负性质求出a和b的值,由平行四边形的对角线互相平分求出平行四边形边长的取值范围,即可得出结论.
解答 解:∵$\sqrt{a-6}$+|b-a+2|=0,
∴a-6=0,b-a+2=0,
∴a=6,b=4,
∴$\frac{1}{2}$a=3,$\frac{1}{2}$b=2,
∴4-3<平行四边形的边长<3+2,
即1<平行四边形的边长<5,
故选:A.
点评 本题考查了平行四边形的性质、算术平方根和绝对值的非负性质、三角形的三边关系;熟练掌握平行四边形的性质和三角形的三边关系,求出a和b是解决问题的关键.

练习册系列答案
相关题目
2.已知方程x2-6x+2=0,该方程用配方法变形后的结果为( )
| A. | (x-6)2=34 | B. | (x+6)2=34 | C. | (x-3)2=7 | D. | (x-3)2=11 |
3.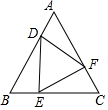 如图,正△ABC的三边上有三点D,E,F,且AD=BE=CF,设AB=x,DE=y,△ADF的内切圆的半径为$\sqrt{3}$,则关于x的函数关系式为( )
如图,正△ABC的三边上有三点D,E,F,且AD=BE=CF,设AB=x,DE=y,△ADF的内切圆的半径为$\sqrt{3}$,则关于x的函数关系式为( )
 如图,正△ABC的三边上有三点D,E,F,且AD=BE=CF,设AB=x,DE=y,△ADF的内切圆的半径为$\sqrt{3}$,则关于x的函数关系式为( )
如图,正△ABC的三边上有三点D,E,F,且AD=BE=CF,设AB=x,DE=y,△ADF的内切圆的半径为$\sqrt{3}$,则关于x的函数关系式为( )| A. | y=x-6 | B. | y=$\frac{\sqrt{3}}{2}x$ | C. | y=x-3 | D. | y=$\frac{\sqrt{3}}{x}$ |

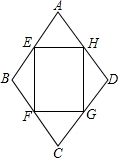 如图,四边形ABCD是一个菱形绿草地,其周长为40$\sqrt{2}$m,∠ABC=120°,在其内部有一个矩形花坛EFGH,其四个顶点恰好在菱形ABCD各边中点,现准备在花坛中种植茉莉花,其单价为30元/2,则需投资资金多少元?($\sqrt{3}$取1.732)
如图,四边形ABCD是一个菱形绿草地,其周长为40$\sqrt{2}$m,∠ABC=120°,在其内部有一个矩形花坛EFGH,其四个顶点恰好在菱形ABCD各边中点,现准备在花坛中种植茉莉花,其单价为30元/2,则需投资资金多少元?($\sqrt{3}$取1.732)