题目内容
17．若|a-b+1|与$\sqrt{a+2b+4}$互为相反数，则（a+b）2的值是9．分析 利用相反数的性质列出关系式，再利用非负数的性质列出方程组，求出方程组的解得到a与b的值，即可求出原式的值．
解答 解：根据题意得：|a-b+1|+$\sqrt{a+2b+4}$=0，
∴$\left\{\begin{array}{l}{a-b=-1}\\{a+2b=-4}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$，
则原式=9，
故答案为：9
点评 此题考查了解二元一次方程组，相反数，以及非负数的性质，熟练掌握运算法则是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，在Rt△ABC中，∠ABC=90°，BA=BC，点D是AB的中点，连接CD，过点B作BG⊥CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连接DF，下面四个结论：①$\frac{FG}{FB}$=$\frac{1}{2}$；②点F是GE的中点；③AF=$\frac{\sqrt{2}}{3}$AB；④S△ABC=6S△BDF．其中正确结论的序号是①③④．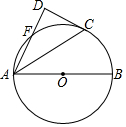
如图．⊙O的半径为5，AB为⊙O直径，C，F为⊙O上的两点，AF，AC为⊙O的弦．