题目内容
3.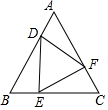 如图,正△ABC的三边上有三点D,E,F,且AD=BE=CF,设AB=x,DE=y,△ADF的内切圆的半径为$\sqrt{3}$,则关于x的函数关系式为( )
如图,正△ABC的三边上有三点D,E,F,且AD=BE=CF,设AB=x,DE=y,△ADF的内切圆的半径为$\sqrt{3}$,则关于x的函数关系式为( )| A. | y=x-6 | B. | y=$\frac{\sqrt{3}}{2}x$ | C. | y=x-3 | D. | y=$\frac{\sqrt{3}}{x}$ |
分析 首先证明△DEF是等边三角形,由S△ADF=S△BDE=S△EFC=$\frac{1}{2}$(AD+AF+DF)•$\sqrt{3}$=$\frac{1}{2}$(x+y)•$\sqrt{3}$,根据S△ABC-S△EDF=3•S△ADF,可得$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{4}$y2=3•$\frac{1}{2}$•(x+y)•$\sqrt{3}$,化简后即可解决问题.
解答 解:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,
又∵∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是一个等边三角形,
∵S△ADF=S△BDE=S△EFC=$\frac{1}{2}$(AD+AF+DF)•$\sqrt{3}$=$\frac{1}{2}$(x+y)•$\sqrt{3}$,
∵S△ABC-S△EDF=3•S△ADF,
∴$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{4}$y2=3•$\frac{1}{2}$•(x+y)•$\sqrt{3}$,
∴(x2-y2)=6(x+y),
∴(x+y)(x-y)=6(x+y),
∵x+y≠0,
∴x-y=6,
∴y=x-6.
故选A.
点评 题主要考查了等边三角形的判定与性质和全等三角形判定及三角形面积公式,根据已知得出△ADF≌△BED≌△CFE是解题关键,解题的突破点是记住S△ABC=$\frac{1}{2}$(a+b+c)•r(r是△ABC内切圆的半径).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.P为直线l上的一点,Q为l外一点,下列说法不正确的是( )
| A. | 过P可画直线垂直于l | B. | 过Q可画直线l的垂线 | ||
| C. | 连结PQ使PQ⊥l | D. | 过Q可画直线与l垂直 |
15.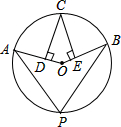 如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )
如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )
 如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )
如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
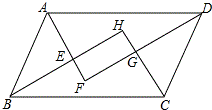 如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.
如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.