题目内容
2.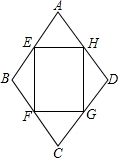 如图,四边形ABCD是一个菱形绿草地,其周长为40$\sqrt{2}$m,∠ABC=120°,在其内部有一个矩形花坛EFGH,其四个顶点恰好在菱形ABCD各边中点,现准备在花坛中种植茉莉花,其单价为30元/2,则需投资资金多少元?($\sqrt{3}$取1.732)
如图,四边形ABCD是一个菱形绿草地,其周长为40$\sqrt{2}$m,∠ABC=120°,在其内部有一个矩形花坛EFGH,其四个顶点恰好在菱形ABCD各边中点,现准备在花坛中种植茉莉花,其单价为30元/2,则需投资资金多少元?($\sqrt{3}$取1.732)
分析 根据菱形的性质,先求出菱形的一条对角线,由三角形的中位线定理,求出矩形的一条边,同理求得另一边,再求出矩形的面积,最后求得投资资金.
解答 解:解:如图,连接AC、BD,
∵∠ABC=120°,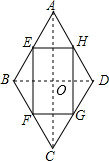
∴∠BAD=180°-120°=60°,
又∵AB=AD,
∴△ABD是等边三角形,
∵菱形的周长是40 $\sqrt{2}$m,
∴AB=40 $\sqrt{2}$÷4=10 $\sqrt{2}$m,
∴OB=$\frac{1}{2}$AB=5 $\sqrt{2}$m,
OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{(10\sqrt{2})^{2}-(5\sqrt{2})^{2}}$=5 $\sqrt{6}$m,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EH=$\frac{1}{2}$BD=OB=5 $\sqrt{2}$m,
EF=$\frac{1}{2}$AC=OA=5 $\sqrt{6}$m,
所以,S矩形EFGH=5 $\sqrt{6}$×5 $\sqrt{2}$=50 $\sqrt{3}$m2,
∵单价是30元/m2,
∴需投入资金30×50 $\sqrt{3}$=1500 $\sqrt{3}$≈2598元.
点评 本题考查了二次根式的应用,勾股定理,菱形的性质,等边三角形的判定与性质,三角形的中位线平行于第三边并且等于第三边的一半,熟记各性质与定理是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
14. 如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
 如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )| A. | (2,-1)或(-2,1) | B. | (8,-4)或(-8,-4) | C. | (2,-1) | D. | (8,-4) |
11.在一些汉字的美术字中,有的是轴对称图形.下面五个词中“自由 平等 民主 敬业 友善”可以看作轴对称图形的汉字有( )个.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则得到的抛物线解析式是( )
| A. | y=(x-2)2-3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x+2)2+3 |
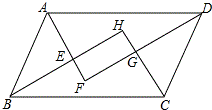 如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.
如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形. 如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.
如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.