题目内容
4.如图所示,△ABC中,∠ACB=90°.BC=AC.BD是∠ABC的角平分线,AE⊥BD,求证:BD=2AE.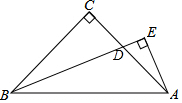
分析 延长AE和BC交于F,根据角平分线的性质得到∠ABE=∠DBC,由垂直的定义得到∠BCD=∠AED=90°,根据全等三角形的性质得到BD=AF,AE=EF,于是得到结论.
解答 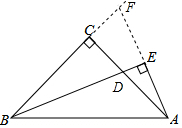 证明:延长AE和BC交于F,
证明:延长AE和BC交于F,
∵∠ACB=90°,
∴∠BCD=∠ACF=90°,
∵BE平分∠ABC,
∴∠ABE=∠DBC,
∵AE⊥BE,
∴∠BCD=∠AED=90°,
∵∠BDC=∠ADE,
∴根据三角形内角和定理得:∠EAD=∠CBD,
在△BCD和△ACF中,
$\left\{\begin{array}{l}{∠DBC=∠CAF}\\{BC=AC}\\{∠BCD=∠ACF}\end{array}\right.$,
∴△BCD≌△ACF(SAS),
∴BD=AF,
在△ABE和△FBE中,$\left\{\begin{array}{l}{∠ABE=∠CBE}\\{BE=BE}\\{∠BEA=∠BEF=90°}\end{array}\right.$,
∴△ABE≌△FBE(ASA),
∴AE=EF,
即AF=2AE,
∴BE=2AE.
点评 本题考查了全等三角形的性质和判定的应用,解此题的关键是求出BD=AF和 AE=EF,题目比较好,难度适中.

练习册系列答案
相关题目
15.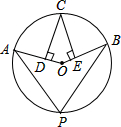 如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )
如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )
 如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )
如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
14. 如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
 如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )| A. | (2,-1)或(-2,1) | B. | (8,-4)或(-8,-4) | C. | (2,-1) | D. | (8,-4) |
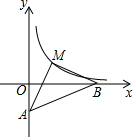 如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,若△AMB是以AB为底的等腰直角三角形,求S△MAB及k的值.
如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,若△AMB是以AB为底的等腰直角三角形,求S△MAB及k的值.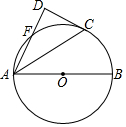 如图.⊙O的半径为5,AB为⊙O直径,C,F为⊙O上的两点,AF,AC为⊙O的弦.
如图.⊙O的半径为5,AB为⊙O直径,C,F为⊙O上的两点,AF,AC为⊙O的弦.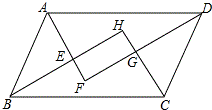 如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.
如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.