题目内容
(1)解下列不等式,并把它们的解集在数轴上表示出来.5x+15>4x-13;
≤
.
(2)解不等式组:
;
(3)求不等式组
的解,并求出不等式组的整数解.
| 2x-1 |
| 3 |
| 3x-4 |
| 6 |
(2)解不等式组:
|
(3)求不等式组
|
考点:解一元一次不等式组,在数轴上表示不等式的解集,解一元一次不等式,一元一次不等式组的整数解
专题:
分析:(1)去分母、去括号,移项合并同类项,即可求解;
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集;
(3)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集,然后确定整数解即可.
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集;
(3)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集,然后确定整数解即可.
解答:解:(1)5x+15>4x-13,
移项,得:5x-4x>-13-15,
合并同类项,得:x>-28.
故解集在数轴上表示出来为:
 ;
;
≤
,
去分母,得:2(2x-1)≤3x-4,
去括号,得:4x-2≤3x-4,
移项,得:4x-3x≤-4+2,
合并同类项,得:x≤-2.
故解集在数轴上表示出来为:
 ;
;
(2)
,
解①得:x<
,
解②得:x>
,
则不等式组的解集是:
<x<
;
(3)
,
解①得:x≥-2,
解②得:x<
,
则不等式组的解集是:-2≤x<
,
则整数解是:-2,-1,0,1,2,3,4,5.
移项,得:5x-4x>-13-15,
合并同类项,得:x>-28.
故解集在数轴上表示出来为:
 ;
;| 2x-1 |
| 3 |
| 3x-4 |
| 6 |
去分母,得:2(2x-1)≤3x-4,
去括号,得:4x-2≤3x-4,
移项,得:4x-3x≤-4+2,
合并同类项,得:x≤-2.
故解集在数轴上表示出来为:
 ;
;(2)
|
解①得:x<
| 10 |
| 3 |
解②得:x>
| 3 |
| 2 |
则不等式组的解集是:
| 3 |
| 2 |
| 10 |
| 3 |
(3)
|
解①得:x≥-2,
解②得:x<
| 11 |
| 2 |
则不等式组的解集是:-2≤x<
| 11 |
| 2 |
则整数解是:-2,-1,0,1,2,3,4,5.
点评:本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
相关题目
数学表达式①-5<7;②3y-6>0;③a=6;④2x-3y;⑤a≠2;⑥7y-6>y+2,其中是不等式的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
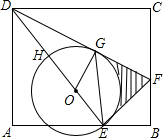 如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F
如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F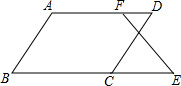 已知:如图,已知∠B+∠BCD=180°,∠B=∠D.那么∠E=∠DFE成立吗?为什么?.
已知:如图,已知∠B+∠BCD=180°,∠B=∠D.那么∠E=∠DFE成立吗?为什么?. 如图,?ABCD的面积等于1,F是BC上一点,AC与DF交于E,已知△CEF的面积为
如图,?ABCD的面积等于1,F是BC上一点,AC与DF交于E,已知△CEF的面积为 如图,网格图中小方格都是边长为1个单位长度的小正方形.
如图,网格图中小方格都是边长为1个单位长度的小正方形.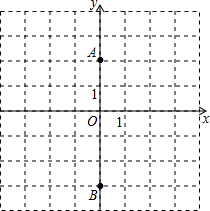 如图,A(0,2),B(0,-3),△ABC的面积为5,点C在x轴上,求点C的坐标.
如图,A(0,2),B(0,-3),△ABC的面积为5,点C在x轴上,求点C的坐标. 如图,已知直线
如图,已知直线