题目内容
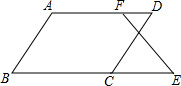 已知:如图,已知∠B+∠BCD=180°,∠B=∠D.那么∠E=∠DFE成立吗?为什么?.
已知:如图,已知∠B+∠BCD=180°,∠B=∠D.那么∠E=∠DFE成立吗?为什么?.下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.
解:∵∠B+∠BCD=180°(已知),
∴
∴∠B=∠DCE(
又∵∠B=∠D(已知 ),
∴∠DCE=∠D (等量代换).
∴AD∥BE(
∴∠E=∠DFE(
考点:平行线的判定与性质
专题:推理填空题
分析:根据平行线的判定推出AB∥CD,根据平行线的性质和已知得出∠DCE=∠D,推出AD∥BE,根据平行线的性质推出即可.
解答:解:∵∠B+∠BCD=180°,
∴AB∥CD(同旁内角互补,两直线平行),
∴∠B=∠DCE(两直线平行,同位角相等),
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE(内错角相等,两直线平行),
∴∠E=∠DFE(两直线平行,内错角相等),
故答案为:AB∥CD,两直线平行,同位角相等,内错角相等,两直线平行,两直线平行,内错角相等.
∴AB∥CD(同旁内角互补,两直线平行),
∴∠B=∠DCE(两直线平行,同位角相等),
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE(内错角相等,两直线平行),
∴∠E=∠DFE(两直线平行,内错角相等),
故答案为:AB∥CD,两直线平行,同位角相等,内错角相等,两直线平行,两直线平行,内错角相等.
点评:本题考查了对平行线的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
命题“两点之间线段最短”是( )
| A、角的定义 | B、假命题 |
| C、公理 | D、定理 |
 周末,小华骑自行车从家里出发到植物园游玩,从家出发0.5小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华离家1小时20分钟后,爸爸开车沿相同路线前往植物园,如图是他们离家的路程y(km)与小华离家时间x(h)的函数图象.已知爸爸开车的速度是小华骑车速度的3倍,若爸爸比小华早10分钟到达植物园,则从小华家到植物园的路程是
周末,小华骑自行车从家里出发到植物园游玩,从家出发0.5小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华离家1小时20分钟后,爸爸开车沿相同路线前往植物园,如图是他们离家的路程y(km)与小华离家时间x(h)的函数图象.已知爸爸开车的速度是小华骑车速度的3倍,若爸爸比小华早10分钟到达植物园,则从小华家到植物园的路程是