题目内容
 如图,?ABCD的面积等于1,F是BC上一点,AC与DF交于E,已知△CEF的面积为
如图,?ABCD的面积等于1,F是BC上一点,AC与DF交于E,已知△CEF的面积为| 1 |
| 40 |
| BF |
| FC |
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:过E的作GH⊥BC,交AD于G,交BC于H,则GH⊥AD,设GH=h,EH=h1,根据△ADE∽△CEF可知AD:FC=(h-h1):h1,然后根据已知条件求得
=
,结合这两个式子得出;h2-hh1-20h1 2=0,从而求得h与h1 的关系,即可求得.
| BC |
| FC |
| 20h1 |
| h |
解答:
解:过E的作GH⊥BC,交AD于G,交BC于H,则GH⊥AD,设GH=h,EH=h1,
∵AD∥BC,
∴△ADE∽△CEF,
∴AD:FC=(h-h1):h1,
∵S△ABC=
BC•h=
,S△EFC=
FC•h1=
,
∴
=
=20,
∴
=
,
∵BC=AD,
∴
=
,
整理得;h2-hh1-20h1 2=0,
解得:h=5h1,h=-4h1 (舍去),
∴
=
=
=
,
即
=
,
∴
=
.

解:过E的作GH⊥BC,交AD于G,交BC于H,则GH⊥AD,设GH=h,EH=h1,
∵AD∥BC,
∴△ADE∽△CEF,
∴AD:FC=(h-h1):h1,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 40 |
∴
| BC•h |
| FC•h1 |
| ||
|
∴
| BC |
| FC |
| 20h1 |
| h |
∵BC=AD,
∴
| 20h1 |
| h |
| h-h1 |
| h1 |
整理得;h2-hh1-20h1 2=0,
解得:h=5h1,h=-4h1 (舍去),
∴
| AD |
| FC |
| h-h1 |
| h1 |
| 5h1-h1 |
| h1 |
| 4 |
| 1 |
即
| BC |
| FC |
| 4 |
| 1 |
∴
| BF |
| FC |
| 3 |
| 1 |
点评:本题考查了相似三角形对应高的比等于相似比,树立数形结合的思想,通过面积公式转化成方程来解决问题.

练习册系列答案
相关题目
下面的图表列出了一项试验的统计数据,表示将皮球从高处h落下,弹跳高度m与下落高度h的关系
试问下面哪个式子能表示这种关系(单位:cm)( )
| h | 50 | 80 | 100 | 150 |
| m | 25 | 40 | 50 | 75 |
| A、m=h2 | ||
| B、m=2h | ||
C、m=
| ||
| D、m=h+25 |
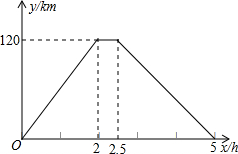 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息回答下列问题:
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息回答下列问题: