题目内容
3.已知:如图1,△ABC内接于⊙O,AF⊥BC交BC于点D,交⊙O于点F,BE⊥AC交AC于点E,交AD于点G.(1)求证:DG=DF;
(2)如图2,当∠ABC=45°时,连接CG,求证:GF=$\sqrt{2}$CG;
(3)在(2)的条件下,如图3,若GC等于⊙O半径,且BG=2,求线段BC的长
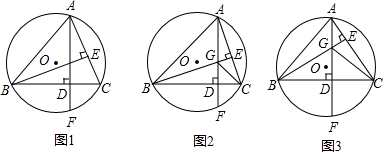
分析 (1)先用等角的余角相等,得出∠CAD=∠CBE,再用同弧所对的圆周角相等,得出∠CAD=∠CBF,即∠DBF=∠DBG,即可得出DG=DF,
(2)先同弧所对的圆周角线段,得出∠AFC=45°,再由(1)得出的结论,利用垂直平分线的性质得出∠DCG=∠DCF,即可得出△CFG是等腰直角三角形,即可得出结论;
(3)先判断出△OCF是等边三角形,从而求出∠CAD=30°,再判断△BDG≌△ADC,得出CD=1,进而用等腰直角三角形的性质和勾股定理求出DG,BD即可.
解答 解:(1)如图1, 连接BF,
连接BF,
∵AF⊥BC交BC于点D,交⊙O于点F,BE⊥AC,
∴∠EAG+∠AGE=90°,∠DBG+∠BGD=90°,
∵∠AGE=∠BGD,
∴∠EAG=∠DBG,
∵∠EAG=∠DBF,
∴∠DBG=∠DBF
∵BC⊥FG,
∴DG=DF(如果三角形一边上的高也是该边所对角的平分线,那么此三角形是等腰三角形),
(2)如图2, 连接CF,
连接CF,
由(1)知,DG=DF,
∵CD⊥FG,
∴CG=CF,∠DCG=∠DCF
∵∠ABC=45°,
∴∠AFC=∠ABC=45°,
∵∠CDF=90°,
∴∠DCG=∠DCF=45°,
∴∠FCG=∠DCF+∠DCG=90°,
在Rt△FCG中,∠CFG=45°,
∴GF=$\sqrt{2}$CG,
(3)如图3,
连接OC,OF,CF,
由(2)知,CG=CF,
∵CG=OC,
∴OC=OF=CG,
∴△OCF是等边三角形,
∴∠COF=60°,
∴∠CAF=$\frac{1}{2}$∠COF=30°,
由(2)∠DCG=45°,∠CDG=90°,
∴∠CGD=45°,
∴∠DCG=∠CGD,
∴DG=DC,
由(1)知,∠DBG=∠DAC
在△BDG和△ADC中,$\left\{\begin{array}{l}{∠DBG=∠DAC}\\{∠BDG=∠ADC=90°}\\{DG=DC}\end{array}\right.$,
∴△BDG≌△ADC,
∴BG=AC,
∵BG=2,
∴AC=2,
在Rt△ACD中,∠CAD=30°,AC=2,
∴CD=1,
∴DG=CD=1,
在Rt△BDG中,BG=2,DG=1,
∴BD=$\sqrt{3}$,
∴BC=BD+CD=$\sqrt{3}$+1.
点评 此题是圆的综合题,主要考查了圆周角的性质,等腰三角形的判定和性质,等腰直角三角形的判定和性质,全等三角形的判定和性质,勾股定理,解本题的关键是判断出△CFG是等腰直角三角形,难点是求出AC.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | (+$\frac{1}{2}$)+(+$\frac{1}{3}$)=$\frac{1}{5}$ | B. | (+$\frac{1}{2}$)+(-$\frac{1}{3}$)=-$\frac{1}{6}$ | C. | (-$\frac{1}{2}$)+(+$\frac{1}{3}$)=$\frac{1}{6}$ | D. | (-$\frac{1}{2}$)+(+$\frac{1}{3}$)=-$\frac{1}{6}$ |
| A. | 1$\frac{1}{2}$ab2 | B. | -$\frac{ab}{2}$ | C. | x+3千米 | D. | ab•3 |
| A. | 6,8,1 | B. | 1,2,$\sqrt{3}$ | C. | 3,4,5 | D. | 1,2,$\sqrt{5}$ |
| A. | 3、4、6 | B. | 24、10、26 | C. | 8、12、15 | D. | 7、9、14 |

 函数y=ax2+bx+c与y=kx的图象如图所示,有以下结论:①b2-4ac>0;②a+b+c=k;③方程ax2+bx+c=kx一定有两个不相等的实数根;④当1<x<3时,ax2+(b-k)x+c<0其中正确的个数为( )
函数y=ax2+bx+c与y=kx的图象如图所示,有以下结论:①b2-4ac>0;②a+b+c=k;③方程ax2+bx+c=kx一定有两个不相等的实数根;④当1<x<3时,ax2+(b-k)x+c<0其中正确的个数为( )