题目内容
13.(1)如图①,A,E,F,C四点在一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,连接BD交AC于点G,若AB=CD,试说明FG=EG.(2)若将△DCE沿AC方向移动变为如图②的图形,(1)中其他条件不变,上述结论是否仍成立?请说明理由.

分析 (1)连接BE、FD,首先由题意推出AF=CE,∠BFA=∠DEC=90°,则由全等三角形的判定定理HL证得Rt△BFA≌Rt△DEC,便知BF=DE,推出四边形BEDF为平行四边形,即可推出BD与EF互相平分,即FG=EG;
(2)同(1)的证明过程.
解答 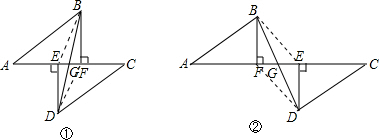 解:(1)连接BE、FD,
解:(1)连接BE、FD,
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
又∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△BFA与Rt△DEC中,
$\left\{\begin{array}{l}{AF=CE}\\{AB=CD}\end{array}\right.$,
∴Rt△BFA≌Rt△DEC(HL),
∴BF=DE,
∵BF∥DE,
∴四边形BEDF为平行四边形,
∴BD与EF互相平分,
∴FG=EG;
(2)上述结论还成立.理由如下:
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
又∵AE=CF,
∴AE-EF=CF-EF,即AF=CE,
在Rt△BFA与Rt△DEC中,
$\left\{\begin{array}{l}{AF=CE}\\{AB=CD}\end{array}\right.$,
∴Rt△BFA≌Rt△DEC(HL),
∴BF=DE,
∵BF∥DE,
∴四边形BEDF为平行四边形,
∴BD与EF互相平分,
∴FG=EG.
点评 本题考查了全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
1.已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm为半径作圆,则这个圆与斜边AB所在直线的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
2.下列二次根式中与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{\frac{1}{9}}$ | B. | $\sqrt{18}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
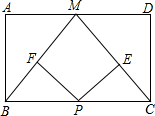 如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.
如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.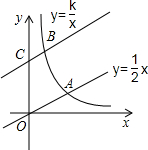 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$.