题目内容
10. 如图,△ABC,AB=8,AC=5,BC=7,AD是△ABC外角平分线,CD⊥AD于D,E是BC的中点,则DE=( )
如图,△ABC,AB=8,AC=5,BC=7,AD是△ABC外角平分线,CD⊥AD于D,E是BC的中点,则DE=( )| A. | 7 | B. | 6.5 | C. | 6 | D. | 5.5 |
分析 延长CD交BA的延长线于F,利用“角边角”证明△ACD和△AFD全等,根据全等三角形对应边相等可得CD=DF,AC=AF,得出AB+AC=BF,证明DE是△BCF的中位线,根据三角形的中位线定理即可得出结果.
解答 解:如图,延长CD交BA的延长线于F,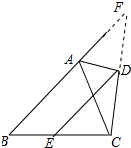
∵AD是△ABC的外角平分线,CD⊥AD,
∴∠CAD=∠FAD,∠ADC=∠ADF=90°,
在△ACD和△AFD中,$\left\{\begin{array}{l}{∠CAD=∠FAD}&{\;}\\{AD=AD}&{\;}\\{∠ADC=∠ADF=90°}&{\;}\end{array}\right.$,
∴△ACD≌△AFD(ASA),
∴CD=DF,AC=AF,
∴AB+AC=BF,
∵E是BC的中点,
∴DE是△BCF的中位线,
∴DE=$\frac{1}{2}$BF=$\frac{1}{2}$(AB+AC)=$\frac{13}{2}$=6.5;
故选:B.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,全等三角形的判定与性质,作辅助线构造出以DE为中位线的三角形是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
1.甲校女生占全校总人数的54%,乙校女生占全校总人数的50%,则女生人数( )
| A. | 甲校多于乙校 | B. | 甲校少于乙校 | C. | 不能确定 | D. | 两校一样多 |
2.石家庄首届中俄国际文化交流暨国家大马戏世界巡演石家庄站的演出活动于2016年正月初三持续至二月初二.若某班45名全体学生去看演出,甲种票每张60元,乙种票每张120元,共花费4140元,则该班学生甲种票共购买了( )
| A. | 21张 | B. | 22张 | C. | 23张 | D. | 24张 |
19. 如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )
如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )
 如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )
如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )| A. | 24 | B. | 28 | C. | 32 | D. | 36 |
20.三角形的三边长分别为a,b,c,且(a-b)2+(a2+b2-c2)2=0,则此三角形的形状为( )
| A. | 任意等腰三角形 | B. | 任意直角三角形 | C. | 任意三角形 | D. | 等腰直角三角形 |
 如图,△ABC中,AB=AC=5,BC=6,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是( )
如图,△ABC中,AB=AC=5,BC=6,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是( )