题目内容
18.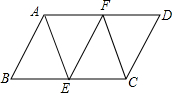 如图,在平行四边形ABCD中,点E、F分别为边BC,AD的中点,则图中共有平行四边形的个数是( )
如图,在平行四边形ABCD中,点E、F分别为边BC,AD的中点,则图中共有平行四边形的个数是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 利用平行四边形的性质得出AD=BC,AD∥BC,进而得出AF$\stackrel{∥}{=}$BE,DF$\stackrel{∥}{=}$EC,AF$\stackrel{∥}{=}$EC,求出答案.
解答 解:∵点E、F分别为边BC,AD的中点,
∴AF=DF,BE=EC,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AF=DF=BE=EC,
∴AF$\stackrel{∥}{=}$BE,DF$\stackrel{∥}{=}$EC,AF$\stackrel{∥}{=}$EC,
∴四边形ABEF是平行四边形,四边形AECF是平行四边形,四边形FECD是平行四边形,
则图中共有平行四边形的个数是4个.
故选:B.
点评 此题主要考查了平行四边形的判定与性质,正确得出AF=DF=BE=EC是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.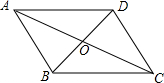 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )| A. | DC=BC | B. | AC⊥BD | C. | AB=BD | D. | ∠ADB=∠CDB |
13. 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )| A. | $\frac{AF}{AB}$=$\frac{AE}{DE}$ | B. | $\frac{AF}{CD}$=$\frac{AE}{BC}$ | C. | $\frac{AF}{AB}=\frac{EF}{CE}$ | D. | $\frac{DE}{AE}=\frac{CE}{EF}$ |
3.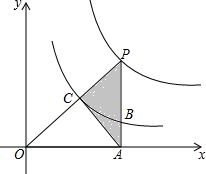 如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )
如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )
 如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )
如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
10.若点(-2,y1),(-1,y2)(1,y3)在反比例函数y=$-\frac{2}{x}$的图象上,则下列结论正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
 如图,在矩形ABCD中,对角线AC、BD相交于点O.求证:AC=BD.
如图,在矩形ABCD中,对角线AC、BD相交于点O.求证:AC=BD.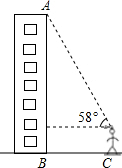 小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)
小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)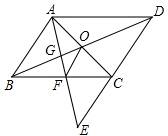 如图,在?ABCD中,F是边BC的中点,连接AF交DC的延长线于点E,AC,BD相交于点O,AF交BD于点G,连接OF,判断EC与OF的位置关系和大小关系,并证明你的结论.
如图,在?ABCD中,F是边BC的中点,连接AF交DC的延长线于点E,AC,BD相交于点O,AF交BD于点G,连接OF,判断EC与OF的位置关系和大小关系,并证明你的结论.