题目内容
19.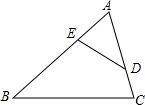 如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )
如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
分析 由∠B+∠CDE=∠C+∠BED,可知∠B+∠CDE=∠C+∠BED=180°,又∠ADE+∠CDE=∠AED+∠BED=180°,可知∠ADE=∠B,∠AED=∠C,于是△AED∽△ACB,根据相似三角形对应边成比例可求出结果.
解答 解:∵∠B+∠CDE=∠C+∠BED,
∴∠B+∠CDE=∠C+∠BED=180°,
又∵∠ADE+∠CDE=∠AED+∠BED=180°,
∴∠ADE=∠B,∠AED=∠C,
∴△AED∽△ACB,
∴$\frac{AE}{AC}=\frac{AG}{AB}$,
∴$\frac{2}{4}=\frac{3}{AB}$,
∴AB=6,
∴BE=AB-AE=6-2=4.
故选D.
点评 本题主要考查了相似三角形的判定与性质,证明∠ADE=∠B,∠AED=∠C是解决问题的关键.

练习册系列答案
相关题目
7.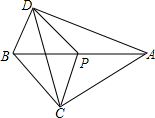 如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )
如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )
 如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )
如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )| A. | 15° | B. | 30° | C. | 25° | D. | 60° |
14. 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
11.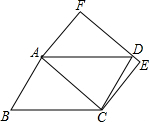 如图,平行四边形ABCD和矩形ACEF的位置如图所示,点D在EF上,则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是( )
如图,平行四边形ABCD和矩形ACEF的位置如图所示,点D在EF上,则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是( )
 如图,平行四边形ABCD和矩形ACEF的位置如图所示,点D在EF上,则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是( )
如图,平行四边形ABCD和矩形ACEF的位置如图所示,点D在EF上,则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | 3S1=2S2 |
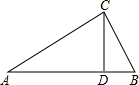 如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高.
如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高. 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1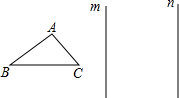 如图,已知△ABC和两条平行直线m、n,画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A″B″C″,如果将△ABC沿着与直线m垂直的方向平移,你会发现什么?
如图,已知△ABC和两条平行直线m、n,画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A″B″C″,如果将△ABC沿着与直线m垂直的方向平移,你会发现什么?