题目内容
2.设等式$\sqrt{a(2x-a)}$+$\sqrt{a(y-a)}$=$\sqrt{2x-a}$-$\sqrt{a-y}$在实数范围内成立,其中a、x、y是两两不等的实数,求代数式$\frac{2{x}^{2}-xy+y^{2}}{3{x}^{2}+xy+{y}^{2}}$的值.分析 根据负数没有平方根,根据已知等式列出不等式,判断得到a=0,把a=0代入得到y=-2x,即可确定出原式的值.
解答 解:由已知等式得:a(2x-a)≥0,a(y-a)≥0,2x-a≥0,a-y≥0,
可得a≥0且a≤0,即a=0,
把a=0代入已知等式得:$\sqrt{2x}$-$\sqrt{-y}$=0,即y=-2x,
则原式=$\frac{2{x}^{2}+2{x}^{2}+4{x}^{2}}{3{x}^{2}-2{x}^{2}+4{x}^{2}}$=$\frac{8}{5}$.
点评 此题考查了二次根式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
13.有四根细木棒,长度分别为3cm,5cm,7cm,9cm,则随机抽出三根木棒,能够组成三角形的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
7.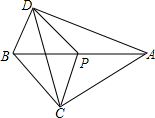 如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )
如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )
 如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )
如图,点P在线段AB上,PA=PB=PC=PD,当∠BPC=60°时,∠BDC=( )| A. | 15° | B. | 30° | C. | 25° | D. | 60° |
14. 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
11.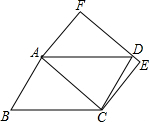 如图,平行四边形ABCD和矩形ACEF的位置如图所示,点D在EF上,则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是( )
如图,平行四边形ABCD和矩形ACEF的位置如图所示,点D在EF上,则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是( )
 如图,平行四边形ABCD和矩形ACEF的位置如图所示,点D在EF上,则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是( )
如图,平行四边形ABCD和矩形ACEF的位置如图所示,点D在EF上,则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | 3S1=2S2 |
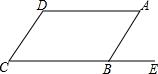 如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C,∠D的度数.
如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C,∠D的度数.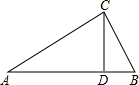 如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高.
如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高.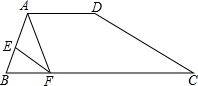 如图,在四边形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于点F,连接AF.
如图,在四边形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于点F,连接AF.