题目内容
5．
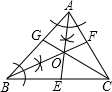如图，AE于BF交于点O，点O在CG上，根据尺规作图的痕迹，判断下列说法不正确的是（ ）| A． | AE、BF是△ABC的内角平分线 | B． | 点O到△ABC三边的距离相等 | ||
| C． | CG也是△ABC的一条内角平分线 | D． | AO=BO=CO |
分析 利用尺规作图的痕迹可得AE、BF是△ABC的内角平分线，即可得出答案．
解答 解：∵由尺规作图的痕迹可得AE、BF是△ABC的内角平分线，
∴点O到△ABC三边的距离相等，CG也是△ABC的一条内角平分线，
故D选项不正确，
故选：D．
点评 本题主要考查了基本作图及角平分线的性质，解题的关键是熟记角平分线的作图方法．
练习册系列答案
相关题目
13．有四根细木棒，长度分别为3cm，5cm，7cm，9cm，则随机抽出三根木棒，能够组成三角形的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
20．如表是某校八年级（8）班共50位同学身高情况的频数分布表，则表中的组距是7，身高最大值与最小值的差至多是27cm．
| 组别（cm） | 145.5～152.5 | 152.5～159.5 | 159.5～166.5 | 166.5～173.5 |
| 频数（人） | 9 | 19 | 14 | 8 |
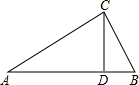如图，在Rt△ABC中，∠C=90°，CD是斜边AB上的高．
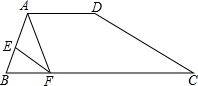如图，在四边形ABCD中，AD∥BC，AE=2EB，AD=2，BC=5，EF∥DC，交BC于点F，连接AF．
14．
如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）
如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）| A． | 2 | B． | 2$\sqrt{3}$ | C． | 4 | D． | 4$\sqrt{2}$ |
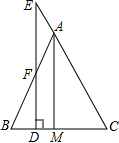如图，在△ABC中，AB=AC，AM是BC边的中线，点E在CA的延长线上，ED∥AM交BC于D，交AB于F，求证：AE=AF．