题目内容
3.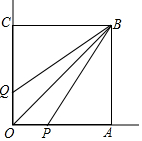 如图,正方形OABC的边长为3,点P与点Q分别在射线OA与射线OC上,且满足BP=BQ,若AP=2,则四边形OPBQ面积的值可能为3或9或15.
如图,正方形OABC的边长为3,点P与点Q分别在射线OA与射线OC上,且满足BP=BQ,若AP=2,则四边形OPBQ面积的值可能为3或9或15.
分析 如图PA=AP′=2,CQ=CQ′=2,①四边形OPBQ的面积=2×$\frac{1}{2}$×1×3=3.②四边形OP′BQ的面积=$\frac{1}{2}$×1×3+$\frac{1}{2}$×5×3=9,③四边形OPBQ′的面积=9.④四边形OP′BQ′的面积=2×$\frac{1}{2}$×5×3=15.四边形有四种可能,面积的值有三种可能.
解答 解: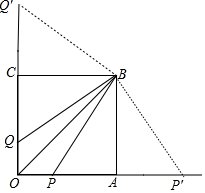
如图PA=AP′=2,CQ=CQ′=2,
①四边形OPBQ的面积=2×$\frac{1}{2}$×1×3=3.
②四边形OP′BQ的面积=$\frac{1}{2}$×1×3+$\frac{1}{2}$×5×3=9,
③四边形OPBQ′的面积=9.
④四边形OP′BQ′的面积=2×$\frac{1}{2}$×5×3=15.
∴四边形OPBQ的面积的值有三种可能.
故答案为3或9或15
点评 本题考查正方形的性质、三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
14.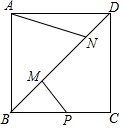 如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )
如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )
 如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )
如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 6 | D. | 3$\sqrt{5}$ |
11.已知代数式-3xm-1y3与5xym+n是同类项,那么m、n的值分别是( )
| A. | m=2,n=-1 | B. | m=-2,n=-1 | C. | m=2,n=1 | D. | m=-2,n=1 |
12.下列运算正确的是( )
| A. | 3a2-a2=2a2 | B. | (a2)3=a5 | C. | a2÷a3=a | D. | a2•a3=a6 |
 如图,将周长为16的三角形ABC沿BC方向平移3个单位得到三角形DEF,则四边形ABFD的周长等于22.
如图,将周长为16的三角形ABC沿BC方向平移3个单位得到三角形DEF,则四边形ABFD的周长等于22.