题目内容
14.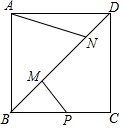 如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )
如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 6 | D. | 3$\sqrt{5}$ |
分析 过P作PE∥BD交CD于E,连接AE交BD于N,过P作PM∥AE交BD于M,此时,AN+PM的值最小,根据三角形的中位线的性质得到PE=$\frac{1}{2}$BD,根据平行四边形的性质得到EN=PM,根据勾股定理得到AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=3$\sqrt{5}$,根据相似三角形的性质即可得到结论.
解答 解:过P作PE∥BD交CD于E,连接AE交BD于N,过P作PM∥AE交BD于M,此时,AN+PM的值最小,
∵P是BC的中点,
∴E为CD的中点,
∴PE=$\frac{1}{2}$BD,
∵AB=$\frac{\sqrt{2}}{2}$BD,AB=$\sqrt{2}$MN,
∴MN=$\frac{1}{2}$BD,
∴PE=MN,
∴四边形PENM是平行四边形,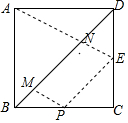
∴EN=PM,
∵AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=3$\sqrt{5}$,
∵AB∥CD,
∴△ABN∽△EDN,
∴$\frac{AN}{NE}$=$\frac{AB}{DE}$=2,
∴AN=2$\sqrt{5}$,
故选B.
点评 本题考查了正方形的性质,轴对称-最短距离问题,平行三角形的判定和性质,三角形的中位线的性质,相似三角形的,正确的作出M,N的位置是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
4.下列运算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$×$3\sqrt{3}$=6$\sqrt{3}$ | C. | $\sqrt{2}$$÷\sqrt{3}$=$\frac{\sqrt{6}}{3}$ | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ |
6.若正比例函数的图象经过点(2,-3),则这个图象必经过点( )
| A. | (-3,-2) | B. | (2,3) | C. | (3,-2) | D. | (-4,6) |
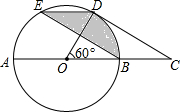 如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为弧AD的中点,连接DE,EB. 若图中阴影部分面积为6π,则⊙O的半径为6.
如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为弧AD的中点,连接DE,EB. 若图中阴影部分面积为6π,则⊙O的半径为6.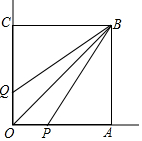 如图,正方形OABC的边长为3,点P与点Q分别在射线OA与射线OC上,且满足BP=BQ,若AP=2,则四边形OPBQ面积的值可能为3或9或15.
如图,正方形OABC的边长为3,点P与点Q分别在射线OA与射线OC上,且满足BP=BQ,若AP=2,则四边形OPBQ面积的值可能为3或9或15.