题目内容
15．一个多边形的内角和是外角和的4倍，这个多边形是十边形，若这个多边形的每个内角都相等，那么每个内角的度数是144°．分析 根据内角和公式，可得答案；根据正多边形，可得答案．
解答 解：设多边形为n边形，由题意，得
（n-2）•180°=360°×4，
解得n=10，
每个内角$\frac{360×4}{10}$=144°，
故答案为：十，144°
点评 本题考查了多边形的内角与外角，利用内角和公式是解题关键．
练习册系列答案
相关题目
6．若正比例函数的图象经过点（2，-3），则这个图象必经过点（ ）
| A． | （-3，-2） | B． | （2，3） | C． | （3，-2） | D． | （-4，6） |
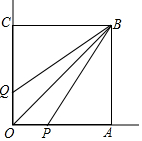如图，正方形OABC的边长为3，点P与点Q分别在射线OA与射线OC上，且满足BP=BQ，若AP=2，则四边形OPBQ面积的值可能为3或9或15．
如图，直线AB，CD交于点O，OA平分∠EOC，∠EOC：∠EOD=4：5，则∠BOD=40度．
5．下列哪一个选项中的等式成立（ ）
| A． | $\sqrt{{2}^{2}}$=2 | B． | $\sqrt{{3}^{3}}$=3 | C． | $\sqrt{{4}^{4}}$=4 | D． | $\sqrt{{5}^{5}}$=5 |