题目内容
在长方形ABCD中,长AB=5,对角线的AC=13,那么矩形ABCD的面积等于 .
考点:矩形的性质
专题:计算题
分析:矩形各内角为90°,∴△ABC为直角三角形,已知AC=13,AB=5,根据勾股定理即可求BC的值,根据AB、BC的值即可求 矩形ABCD的面积.
解答:解:∵矩形各内角为90°,
∴△ABC为直角三角形,
AC=13,AB=5,
∴BC=
=12,
故长方形ABCD的面积=5×12=60.
故答案为 60.
∴△ABC为直角三角形,
AC=13,AB=5,
∴BC=
| AC2-AB2 |
故长方形ABCD的面积=5×12=60.
故答案为 60.
点评:本题考查了矩形面积的计算,考查了勾股定理在直角三角形中的运用,本题中根据勾股定理计算BC的长是解题的关键.

练习册系列答案
相关题目
抛物线y=mx2+x和y=nx2+x与x轴正半轴分别交于点A和点B.若点A在点B的右边,则m与n的大小关系为( )
| A、m>n | B、m<n |
| C、m=n | D、无法确定 |
 如图,△ABC的边AB=30cm,AC=25cm,点D、F在AC上,点E、G在AB上,S△ADE:S△DEF:S△EFG:S△FGC:S△GBC=1:2:3:4:5(S△XYZ表示△XYZ的面积).求AD和EG的长.
如图,△ABC的边AB=30cm,AC=25cm,点D、F在AC上,点E、G在AB上,S△ADE:S△DEF:S△EFG:S△FGC:S△GBC=1:2:3:4:5(S△XYZ表示△XYZ的面积).求AD和EG的长.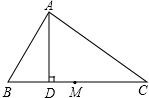 如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,AB=10厘米,则MD的长为
如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,AB=10厘米,则MD的长为 如图,矩形ABCD中,E,F分别是BC,CD上的点,且S△ABE=2,S△CEF=3,S△ADF=4,则S△AEF=
如图,矩形ABCD中,E,F分别是BC,CD上的点,且S△ABE=2,S△CEF=3,S△ADF=4,则S△AEF= 如图,平行四边形ABCD中,∠A是它的外角的
如图,平行四边形ABCD中,∠A是它的外角的