题目内容
如图，△ABC的边AB=30cm，AC=25cm，点D、F在AC上，点E、G在AB上，S△ADE：S△DEF：S△EFG：S△FGC：S△GBC=1：2：3：4：5（S△XYZ表示△XYZ的面积）．求AD和EG的长．考点：三角形的面积
专题：计算题
分析：设AD=xcm，AE=ycm．根据三角形的面积比求得线段之间的关系，再进一步列方程求解．
解答：解：设AD=xcm．
∵S△ADE：S△DEF：S△EFG：S△FGC：S△GBC=1：2：3：4：5，
∴DF=2x，S△AEF：S△EFG=1：1，S△AFG：S△ACG=6：4=3：2，
∵AF=3x，FC=2x．
则2x+3x=25，
x=5．
设AE=ycm．
∵S△ADE：S△DEF：S△EFG：S△FGC：S△GBC=1：2：3：4：5，
∴EG=y，AG=2y，BG=y，
则2y+y=30，
又y=10．
所以AD=5cm，EG=10cm．
∵S△ADE：S△DEF：S△EFG：S△FGC：S△GBC=1：2：3：4：5，
∴DF=2x，S△AEF：S△EFG=1：1，S△AFG：S△ACG=6：4=3：2，
∵AF=3x，FC=2x．
则2x+3x=25，
x=5．
设AE=ycm．
∵S△ADE：S△DEF：S△EFG：S△FGC：S△GBC=1：2：3：4：5，
∴EG=y，AG=2y，BG=y，
则2y+y=30，
又y=10．
所以AD=5cm，EG=10cm．
点评：掌握三角形的面积比和底的比之间的关系：等高的两个三角形的面积比等于它们的底的比．
练习册系列答案
相关题目
方数是指一个整数的平方）
如图，等腰梯形ABCD中，上底AD=5cm，下底BC=8cm，以CD为边向外作正方形CDEF，则△EAD的面积等于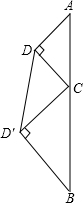
如图，直线段AB的长为l，C为AB上的一个动点，分别以AC和BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCD′，那么DD′的长的最小值为自圆外一点P引圆的两条割线PAB、PCD，连接AC、BD、AD、BC，则图中相似三角形的对数是（ ）
| A、2对 | B、3对 | C、4对 | D、5对 |