题目内容
有若干个大小相同的球,可将它们摆成正方形(充满)或正三角形(充满),摆成正三角形时比摆成正方形时每边多两个球,求球的个数.
考点:一元二次方程的应用
专题:几何图形问题
分析:设出小球摆成正三角形时,每边球的个数,表示出摆成正方形时每边球的个数,分别求出摆成正三角形和正方形时球的总个数,联立方程即可解答.
解答:解:设小球摆成正三角形时,每边有x个球,则摆成正方形时每边有(x-2)个球.
此时正三角形共有球:1+2+3+4+…+x=
个;
此时正方形共有球:(x-2)2个;
所以
=(x-2)2,
即x2-9x+8=0,
解得x1=1,x2=8,
因为x-2≥1,
所以x1=1不符合题意,舍去.
所以x=8,此时共有球(x-2)2=36个.
答:球的个数为36个.
此时正三角形共有球:1+2+3+4+…+x=
| x(x+1) |
| 2 |
此时正方形共有球:(x-2)2个;
所以
| x(x+1) |
| 2 |
即x2-9x+8=0,
解得x1=1,x2=8,
因为x-2≥1,
所以x1=1不符合题意,舍去.
所以x=8,此时共有球(x-2)2=36个.
答:球的个数为36个.
点评:此题主要考查连续自然数的计算方法:1+2+3+…+n=
,解答时注意数形结合.
| n(n+1) |
| 2 |

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
自圆外一点P引圆的两条割线PAB、PCD,连接AC、BD、AD、BC,则图中相似三角形的对数是( )
| A、2对 | B、3对 | C、4对 | D、5对 |
与在数轴上表示数2的点距离等于3个单位的点所表示的数是( )
| A、-1 | B、5 |
| C、3或-3 | D、-1或5 |
已知
=
=
,且a,b,c互不相等,则x+y+z等于( )
| a-b |
| x |
| b-c |
| y |
| c-a |
| z |
| A、a+b-c | ||
| B、0 | ||
C、
| ||
| D、1 |
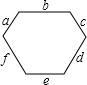 如图,一个凸六边形的六个内角都是120°,六条边的长分别为a,b,c,d,e,f,则下列等式中成立的是( )
如图,一个凸六边形的六个内角都是120°,六条边的长分别为a,b,c,d,e,f,则下列等式中成立的是( )| A、a+b+c=d+e+f |
| B、a+c+e=b+d+f |
| C、a+b=d+e |
| D、a+c=b+d |