题目内容
15.已知抛物线y=ax2+bx+c顶点坐标为(4,-1),与y轴交于点(0,3),求这条抛物线的解析式.分析 设这条抛物线的解析式为y=a(x-4)2-1,代入点(0,3),根据待定系数法即可求得.
解答 解:设这条抛物线的解析式为y=a(x-4)2-1,
把点(0,3)代入y=a(x-4)2-1得a=$\frac{1}{4}$,
∴这条抛物线的解析式为y=$\frac{1}{4}$(x-4)2-1
即y=$\frac{1}{4}$x2-2x+3.
点评 本题考查了待定系数法求二次函数的解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
7.某校有A、B、C三个餐厅,甲.乙两名学生各自随机选择其中的一个餐厅用餐,则甲.乙两名学生在同一个餐厅用餐的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
4.在有理数0,-5,-$\frac{2}{3}$,|-2|中,最小的数是( )
| A. | -$\frac{2}{3}$ | B. | -5 | C. | 0 | D. | |-2| |
5.要调查下面的问题,适合做全面调查的是( )
| A. | 某型号节能灯的使用寿命 | B. | 某水库中鱼的种类 | ||
| C. | 某鞋厂生产的鞋底承受的弯折次数 | D. | 某班同学“立定跳远”的成绩 |
 如图,在四边形ABCD中,对角线AC与BD相交于点O,AO=CO,E,F是AC上的两点,且AE=CF,BE∥DF.
如图,在四边形ABCD中,对角线AC与BD相交于点O,AO=CO,E,F是AC上的两点,且AE=CF,BE∥DF.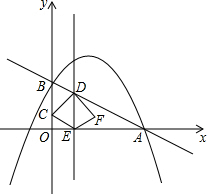 如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,抛物线y=-$\frac{1}{2}$x2+bx+c经过A,B两点.
如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,抛物线y=-$\frac{1}{2}$x2+bx+c经过A,B两点.