题目内容
20.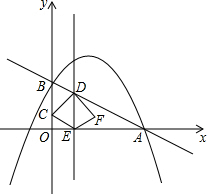 如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,抛物线y=-$\frac{1}{2}$x2+bx+c经过A,B两点.
如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,抛物线y=-$\frac{1}{2}$x2+bx+c经过A,B两点.(1)求抛物线的解析式;
(2)动点C,E从原点O同时出发,C以每秒1个单位长度的速度沿OB方向运动,E以每秒2个单位长度的速度沿OA方向运动,运动时间是t秒(0<t<2).过E点作DE⊥OA交AB于D,C关于DE的对称点为F,连接CD,CE,FD,FE,四边形CDEF与△ABO重叠部分的面积为S.
①求S与t的函数关系式;
②当△BCD为直角三角形时,直接写出t的值.
分析 (1)根据自变量与函数值的对应关系,可得A、B点坐标,根据待定系数法,可得函数解析式;
(2)①分类讨论:0<t≤$\frac{2}{3}$时,根据三角形的面积公式,可得答案;当$\frac{2}{3}$<t<2时,根据面积的和差,可得答案;
②当∠BCD=90°时根据CD的纵坐标相等,可得关于t的方程,根据解方程,可得答案;当∠CDB=90°时,根据相似三角形的判定与性质,可得关于t的方程,可得答案.
解答 解:(1)当x=0时,y=2,即B(0,2),
当y=0时,x=4,即A(4,0).
将A、B点代入抛物线的解析式,得
$\left\{\begin{array}{l}{-\frac{1}{2}×{4}^{2}+4b+c=0}\\{c=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=\frac{3}{2}}\\{c=2}\end{array}\right.$,
抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
(2)如图1: ,
,
①F(4t,t),
当F在AB上时,t=-$\frac{1}{2}$×4t+2,
解得t=$\frac{2}{3}$;
当0<t≤$\frac{2}{3}$时,S=$\frac{1}{2}$×4t×(-$\frac{1}{2}$×2t+2)=-2t2+4t;
当$\frac{2}{3}$<t<2时,S=S△CDE+S△IDE,
S△CDE=$\frac{1}{2}$×(-$\frac{1}{2}$×2t+2)×2t=-t2+2t.
S△IDE=$\frac{1}{2}$(-$\frac{1}{2}$×2t+2)×IH.
∵$\frac{IH}{DH}$=$\frac{IH}{EH}$=$\frac{4}{2}$=2,
∴IH=DE=-$\frac{1}{2}$×2t+2,
S△IDE=$\frac{1}{2}$×(-$\frac{1}{2}$×2t+2)2=$\frac{1}{2}$t2-2t+2,
S=-t2+2t+$\frac{1}{2}$t2-2t+2=-$\frac{1}{2}$t2+2;
②如图2: ,
,
当∠BCD=90°时,C、D的纵坐标相等,即
-$\frac{1}{2}$×2t+2=t,
解得t=1;
当∠CDB=90°时,如图3: ,
,
G(2t,2),D(2t,2-t),H(2t,2-2t),
$\frac{DG}{CH}$=$\frac{BG}{DH}$,即$\frac{t}{2t}$=$\frac{2t}{2-2t}$,
化简,得6t2-2t=0,
解得t=$\frac{1}{3}$,t=0(不符合题意的解要舍去).
综上所述:t=1或t=$\frac{1}{3}$,△BCD为直角三角形.
点评 本题考查了二次函数的综合题,(1)利用待定系数法求函数解析式;(2)①要分类讨论,以防遗漏,利用面积的和差是解题关键;②利用了相似三角形的判定与性质.

 名校课堂系列答案
名校课堂系列答案| A. | a5 | B. | a6 | C. | a8 | D. | a9 |




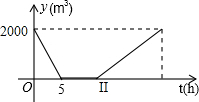 某游泳池内现存水2000m3,已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水-清洗-灌水”的过程,其中游泳池内剩余的水量ym3与换水时间th之间的函数关系如图所示.根据图象解答下列问题:
某游泳池内现存水2000m3,已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水-清洗-灌水”的过程,其中游泳池内剩余的水量ym3与换水时间th之间的函数关系如图所示.根据图象解答下列问题: