题目内容
已知反比例函数y1=-
与一次函数y2=-x+2的图象交于A、B两点(点B在点A的右侧).
(1)求A、B两点的坐标;
(2)当y1<y2时,求x的取值范围.
| 8 |
| x |
(1)求A、B两点的坐标;
(2)当y1<y2时,求x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)将反比例函数y1=-
与一次函数y2=-x+2组成方程组得到A、B两点坐标;
(2)由两函数交点坐标,根据图象求出x的取值范围.
| 8 |
| x |
(2)由两函数交点坐标,根据图象求出x的取值范围.
解答: 解:(1)将反比例函数y1=-
解:(1)将反比例函数y1=-
与一次函数y2=-x+2组成方程组得,
,
解得
或
.
则A(-2,4),B(4,-2).
(2)如图:当y1<y2时,x的取值范围是x<-2或0<x<4.
 解:(1)将反比例函数y1=-
解:(1)将反比例函数y1=-| 8 |
| x |
|
解得
|
|
则A(-2,4),B(4,-2).
(2)如图:当y1<y2时,x的取值范围是x<-2或0<x<4.
点评:本题考查了反比例函数与一次函数的交点问题,熟悉函数图象及解析式与函数图象交点的坐标之间的关系是解题的关键.

练习册系列答案
相关题目
若代数式
有意义,则实数x的取值范围是( )
| ||
| x+1 |
| A、x≠-1 | B、x≥0 |
| C、x>0 | D、x≤0且x≠-1 |
 已知:如图,圆O中的弦AB、CD的延长线交于点P,且DA=DP.求证:BC=BP.
已知:如图,圆O中的弦AB、CD的延长线交于点P,且DA=DP.求证:BC=BP.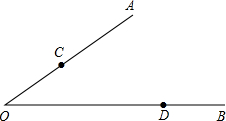 画图:如图,已知点C、点D分别在∠AOB的边上,请根据下列语句画出图形:
画图:如图,已知点C、点D分别在∠AOB的边上,请根据下列语句画出图形: 如图,在?ABCD中,延长AD至点F,延长CB至点E,使DF=BE,求证:AE∥CF.
如图,在?ABCD中,延长AD至点F,延长CB至点E,使DF=BE,求证:AE∥CF.