题目内容
己知a+b=14，a2+b2=4，求a2b2与（a-b）2的值．
考点：完全平方公式
专题：计算题
分析：将a+b=14两边平方，利用完全平方公式展开，将a2+b2=4代入求出ab的值，即可确定出a2b2的值，再利用完全平方公式计算即可得到（a-b）2的值．
解答：解：将a+b=14两边平方得：（a+b）2=a2+b2+2ab=196，
将a2+b2=4代入得：4+2ab=196，即ab=96，
则a2b2=9216；（a-b）2=a2+b2-2ab=4-192=-188．
将a2+b2=4代入得：4+2ab=196，即ab=96，
则a2b2=9216；（a-b）2=a2+b2-2ab=4-192=-188．
点评：此题考查了完全平方公式，熟练掌握公式是解本题的关键．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
如图，正方形ABCD内接于⊙O，它的边长为4cm，则⊙O的半径是（ ）A、2
| ||
B、4
| ||
| C、2cm | ||
| D、4cm |
若a≠0，则下列计算中正确的是（ ）
| A、a2•a3=a6 |
| B、a3+2a3=3a3 |
| C、a6÷a2=a3 |
| D、（a2）3=a5 |
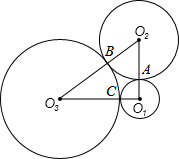如图所示，⊙O1、⊙O2、⊙O3两两外切，切点为A、B、C，它们的半径为r1、r2、r3．
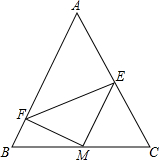如图，在△ABC中，M是BC的中点，E，F分别在AC，AB上，且ME⊥MF．求证：EF＜BF+CE．