题目内容
14.等腰△ABC的三个顶点都在⊙O上,底边BC=8cm,⊙O的半径为5cm,则△ABC的面积为32或8.分析 作AD⊥BC于D,根据等腰三角形的性质得BD=CD=$\frac{1}{2}$BC=4,即AD垂直平分BC,根据垂径定理得到圆心O在AD上;连结OD,在Rt△OBC中利用勾股定理计算出OD=3,然后分类讨论:当△ABC为锐角三角形时,AD=OA+OD=8;当△ABC为钝角三角形时,AD=OA-OD=2,再根据三角形面积公式分别进行计算.
解答 解: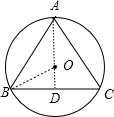 作AD⊥BC于D,
作AD⊥BC于D,
∵AB=AC,
∴BD=CD=$\frac{1}{2}$BC=4,
∴AD垂直平分BC,
∴圆心O在AD上,
连结OD,
在Rt△OBC中,∵BD=4,OB=5,
∴OD=$\sqrt{O{B}^{2}-B{D}^{2}}$=3,
当△ABC为锐角三角形时,AD=OA+OD=5+3=8,此时S△ABC=$\frac{1}{2}$×8×8=32;
当△ABC为钝角三角形时,AD=OA-OD=5-3=2,此时S△ABC=$\frac{1}{2}$×8×2=8.
故答案为:32或8.
点评 本题考查了垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰三角形的性质和勾股定理.

练习册系列答案
相关题目
4.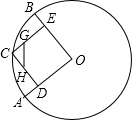 在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )
在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )
 在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )
在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变 | D. | 不能确定 |
19.(-3)2的平方根是( )
| A. | -3 | B. | 3 | C. | 3或-3 | D. | 9 |
6.已知点A(-4,y1),B(2,y2)都在双曲线y=$\frac{k}{x}$(k>0)上,则y1、y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
 长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.
长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.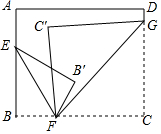 如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°.
如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°.