题目内容
15.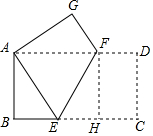 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )| A. | 5cm | B. | $2\sqrt{5}$cm | C. | 2$\sqrt{3}$cm | D. | $3\sqrt{5}$cm |
分析 依据翻折的性质可得到AE=EC,设BE=x,则AE=EC=8-x,在Rt△ABE中,依据勾股定理可求得x的值,则可得到BE、AE的长,然后再证明AE=AF=5,从而可求得EH的长,最后在Rt△EFH中,依据勾股定理可求得EF的长.
解答 解:如图所示:过点F作FH⊥BC,垂足为H.
由翻折的性质可知AE=EC.
设BE=x,则AE=EC=8-x.
在Rt△ABE中,依据勾股定理得:42+x2=(8-x)2,解得:x=3.
∴BE=3,AE=5.
由翻折的性质可知:∠AEF=∠CEF.
∵AF∥BH,
∴∠AFE=∠FEC.
∴∠AFE=∠AEF.
∴AF=AE=5.
∴BH=5.
∴EH=2.
∵HF=AB=4.
∴EF=$\sqrt{E{H}^{2}+F{H}^{2}}$=2$\sqrt{5}$.
故选:B.
点评 本题主要考查的是矩形的性质、翻折的性质、勾股定理的应用,求得EH、FH的长是解题的关键.

练习册系列答案
相关题目
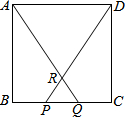 如图,正方形ABCD中,P,Q是BC边上的三等分点,连接AQ、DP交于点R.若正方形ABCD的面积为144cm2,则△PQR的面积为6cm2.
如图,正方形ABCD中,P,Q是BC边上的三等分点,连接AQ、DP交于点R.若正方形ABCD的面积为144cm2,则△PQR的面积为6cm2.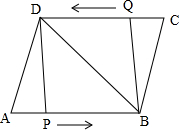 如图,已知?ABCD中,AD=8cm,AB=10cm,BD=12cm,点P从点A出发,以1cm/s的速度向点B运动,同时点Q从点C出发以相同的速度向点D运动,设运动时间为t.
如图,已知?ABCD中,AD=8cm,AB=10cm,BD=12cm,点P从点A出发,以1cm/s的速度向点B运动,同时点Q从点C出发以相同的速度向点D运动,设运动时间为t.
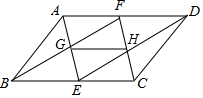 如图所示,在?ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H.求证:GH$\stackrel{∥}{=}$$\frac{1}{2}$AD.
如图所示,在?ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H.求证:GH$\stackrel{∥}{=}$$\frac{1}{2}$AD.