题目内容
15.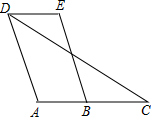 已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.
已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.求证:∠A=∠E.
证明:∵∠EDC=∠C,
∴AB∥DE.(内错角相等,两直线平行)
∴∠E=∠EBC.(两直线平行,内错角相等)
∵AD∥BE,
∴∠A=∠EBC.(两直线平行,同位角相等)
∴∠A=∠E.(等量代换)
分析 根据平行线的判定得出AB∥DE,根据平行线的性质得出∠E=∠EBC,∠A=∠EBC,即可得出答案.
解答 证明:∵∠EDC=∠C,
∴AB∥DE(内错角相等,两直线平行),
∴∠E=∠EBC(两直线平行,内错角相等),
∵AD∥BE,
∴∠A=∠EBC(两直线平行,同位角相等),
∴∠A=∠E.(等量代换),
故答案为:DE,内错角相等,两直线平行,∠E,∠EBC,两直线平行,内错角相等,∠EBC,两直线平行,同位角相等.
点评 本题考查了平行线的性质和判定,能熟练地运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
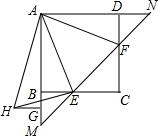 如图,在矩形ABCD中,点E、F分别在边BC、CD上,且EF分别与AB、AD的延长线交于点M、N,∠EAF=∠CEF=45°.点G在边AB的延长线上,将△ADF绕着点A按顺时针方向旋转90°后能与△AGH重合,连接EH.
如图,在矩形ABCD中,点E、F分别在边BC、CD上,且EF分别与AB、AD的延长线交于点M、N,∠EAF=∠CEF=45°.点G在边AB的延长线上,将△ADF绕着点A按顺时针方向旋转90°后能与△AGH重合,连接EH.
 由菱形ABCD向外作四个正方形,若菱形ABCD与八边形的面积之比为1:11,则这个八边形每个内角的度数分别是105°,165°.
由菱形ABCD向外作四个正方形,若菱形ABCD与八边形的面积之比为1:11,则这个八边形每个内角的度数分别是105°,165°.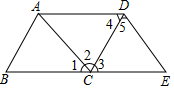 如图,点E在BC的延长线上,下列条件中,
如图,点E在BC的延长线上,下列条件中,