题目内容
(1)将抛物线y1=2x2向右平移2个单位,得到抛 物线y2的图象,则y2=2(x﹣2)2或2x2﹣8x+8;
物线y2的图象,则y2=2(x﹣2)2或2x2﹣8x+8;
(2)如图,P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则

t=1,3或 . 解:(1)抛物线y1=2x2向右平移2个单位,得:y=2(x﹣2)2=2x2﹣8x+8;
. 解:(1)抛物线y1=2x2向右平移2个单位,得:y=2(x﹣2)2=2x2﹣8x+8;
故抛物线y2的解析式为y2=2x2﹣8x+8.

(2)由(1)知:抛物线y2的对称轴为x=2,故P点横坐标为2;
当x=t时,直线y=x=t,故A(t,t);
则y2=2x2﹣8x+8=2t2﹣8t+8,故B(t,2t2﹣8t+8);
若△ABP是以点A或点B为直角顶点的等腰直角三角形,则有AB=AP或AB=BP,
此时AB=|2t2﹣8t+8﹣t|,AP=|t﹣2|,
可得:|t﹣2 |=|2t2﹣8t+8﹣t|;
|=|2t2﹣8t+8﹣t|;
当2t2﹣8t+8﹣t=t﹣2时,如图1,t2﹣5t+5=0,解得t1= ;
;
当2t2﹣8t+8﹣t=2﹣t时,如图2,t2﹣4t+3=0,解得t2=1,t3=3;
故符合条件的t值为:1或3或 .
.



练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 。
。
 C.
C.  D. 2
D. 2 B.
B. C.
C. D.
D.
 ,1.010010001…(每两个1之间依次多一个0),3.
,1.010010001…(每两个1之间依次多一个0),3.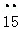 ,
, 中,有理数的个数为( )
中,有理数的个数为( )
 B. 6 C.
B. 6 C.  D. 3
D. 3