题目内容
1.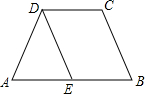 如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC
如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC(1)求证:AB∥CD;
(2)过点D作DE∥BC交AB于点E,若∠ADC-∠A=60°,请判断△ADE是哪种特殊的三角形,并说明理由.
分析 (1)根据四边形内角和定理求出∠A+∠ADC=180°,根据平行线的判定推出即可;
(2)求出∠A=60°,求出∠B=60°,根据平行线的性质求出∠DEA=60°,根据等边三角形的判定推出即可.
解答 (1)证明:∵四边形ABCD中,∠A=∠B,∠C=∠ADC,
∴∠A+∠B+∠C+∠ADC=2∠A+2∠ADC=360°,
∴∠A+∠ADC=180°,
∴AB∥DC;
(2)是等边三角形,
理由是:∵∠A+∠ADC=180°,∠ADC-∠A=60°,
∴∠A=60°,
∵∠B=∠A,
∴∠B=60°,
∵DE∥BC,
∴∠DEA=∠B=60°,
∴AD=DE,
∴△ADE是等边三角形(有一个角是60°的等腰三角形是等边三角形).
点评 本题考查了平行线的性质和判定,四边形的内角和定理,等边三角形的性质和判定的应用,解此题的关键是求出∠A的度数和得出∠A+∠ADC=180°,此题是一道中档题目.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,则∠BMC的度数为150°.
如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,则∠BMC的度数为150°.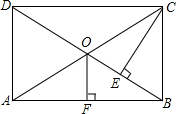 如图,矩形ABCD的对角线AC、BD相交于点O,CE⊥BD,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长.
如图,矩形ABCD的对角线AC、BD相交于点O,CE⊥BD,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长.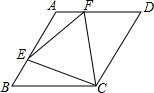 已知如图,在菱形ABCD中,∠B=60°,点E、F分别在AB、AD上,且BE=AF.求证:△ECF是等边三角形.
已知如图,在菱形ABCD中,∠B=60°,点E、F分别在AB、AD上,且BE=AF.求证:△ECF是等边三角形.