题目内容
10.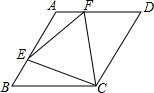 已知如图,在菱形ABCD中,∠B=60°,点E、F分别在AB、AD上,且BE=AF.求证:△ECF是等边三角形.
已知如图,在菱形ABCD中,∠B=60°,点E、F分别在AB、AD上,且BE=AF.求证:△ECF是等边三角形.
分析 连接AC,由菱形的性质可证明△ACE≌△CDF,得出EC=FC,再证出∠ECF=60°,根据有一个角是60°的等腰三角形是等边三角形即可得出结论.
解答 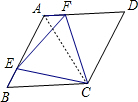 解:连接AC,
解:连接AC,
∵四边形ABCD是菱形,
∴AB=BC=AD=CD,
∵∠B=60°,
∴∠D=∠B=60°,∠BCD=120°,△ABC是等边三角形,
∴∠BAC=60°,AC=AB,
∴AC=CD,
∵BE=AF,
∴AE=DF,
在△ACE与△DCF中,$\left\{\begin{array}{l}{AC=CD}&{\;}\\{∠BAC=∠D}&{\;}\\{AE=DF}&{\;}\end{array}\right.$,
∴△ACE≌△DCF(SAS),
∴EC=FC.∠ACE=∠DCF,
∵∠DCF+∠ACF=60°,
∴∠ACE+∠ACF=60°,
即∠ECF=60°,
∴△ECF是等边三角形.
点评 本题考查了菱形的性质、等边三角形的判定与性质、全等三角形的判定与性质;熟练掌握菱形的性质,通过证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
相关题目
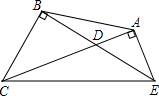 如图,△CDE中,∠CDE=135°,CB⊥DE于B,EA⊥CD于A,求证:CE=$\sqrt{2}$AB.
如图,△CDE中,∠CDE=135°,CB⊥DE于B,EA⊥CD于A,求证:CE=$\sqrt{2}$AB.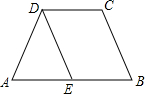 如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC
如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC 如图△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是5.
如图△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是5.