题目内容
6. 如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,则∠BMC的度数为150°.
如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,则∠BMC的度数为150°.
分析 以AC为边作对边△BCE,使A,E在BC的同侧,连接AE,利用全等三角形证得角与角的关系,AB=BD,得到等腰三角形,由等边对等角,三角形的内角和求解.
解答 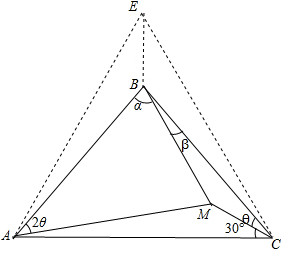 解:以AC为边作等边△ACE,使B,E在AC的同侧,连接BE,
解:以AC为边作等边△ACE,使B,E在AC的同侧,连接BE,
设∠BCM=θ,∠ABM=α,∠CBM=β,
在△ABE与△BCE中,$\left\{\begin{array}{l}{AE=CE}\\{BE=BE}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCE,
∴∠AEB=∠BEC=30°=∠ACM,
∵∠BAE=∠EAC-∠BAM-∠MAC=30°-θ=∠MAC,
在△ABE与△AMC中,$\left\{\begin{array}{l}{∠AEB=∠ACM}\\{∠ABE=∠AMC}\\{AE=AC}\end{array}\right.$,
∴△ABE≌△MAC,
∴AB=AM,
∴α=∠ABM=$\frac{1}{2}$(180°-∠BAM)=90°-θ,
∴β=180°-∠BAC-∠BCA-α=30°-θ,
∴∠BMC=180°-β-θ=150°.
点评 本题考查了等腰三角形的性质和判定,等边三角形的性质,全等三角形的判定与性质,解题的关键是角与角之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.方程组$\left\{\begin{array}{l}{x+y=1}\\{2y-x=8}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-3}\\{y=4}\end{array}\right.$ |
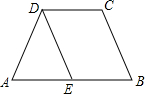 如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC
如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC 如图△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是5.
如图△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是5.