题目内容
9.先化简,再求值:(x+$\frac{2xy+{y}^{2}}{x}$)÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-xy}$,其中x=-2015,y=2014.分析 先计算括号里面的,再将除法转化为乘法,因式分解后约分.
解答 解:原式=$\frac{{x}^{2}+2xy+{y}^{2}}{x}$×$\frac{x(x-y)}{(x-y)(x+y)}$
=$\frac{(x+y)^{2}}{x}$×$\frac{x(x-y)}{(x-y)(x+y)}$
=x+y,
当x=-2015,y=2014时,
原式=-2015+2014=-1.
点评 本题考查了分式的化简求值,熟悉通分、约分、因式分解是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图所示,一次函数y=kx+b的图象经过A、B两点,则kx+b>0的解集是x>-3.
如图所示,一次函数y=kx+b的图象经过A、B两点,则kx+b>0的解集是x>-3.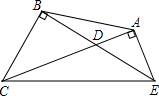 如图,△CDE中,∠CDE=135°,CB⊥DE于B,EA⊥CD于A,求证:CE=$\sqrt{2}$AB.
如图,△CDE中,∠CDE=135°,CB⊥DE于B,EA⊥CD于A,求证:CE=$\sqrt{2}$AB.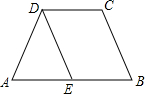 如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC
如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC