题目内容
11.计算;$\left\{\begin{array}{l}{x-3(x-2)≥4}\\{\frac{2x-1}{5}>\frac{x+1}{2}}\end{array}\right.$.分析 首先分别计算出两个不等式的解集,再根据同小取小确定不等式组的解集.
解答 解:$\left\{\begin{array}{l}{x-3(x-2)≥4①}\\{\frac{2x-1}{5}>\frac{x+1}{2}②}\end{array}\right.$,
由①得:x≤1,
由②得:x<-7,
不等式组的解集为:x<-7.
点评 此题主要考查了一元一次不等式组的解法,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
16.方程组$\left\{\begin{array}{l}{x+y=1}\\{2y-x=8}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-3}\\{y=4}\end{array}\right.$ |
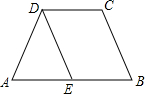 如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC
如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC