题目内容
16.已知菱形的边长为6cm,一个角为60°,求菱形的两条对角线的长.分析 先根据菱形的性质证明△ABC是等边三角形,得出AC=AB,∠BAO=60°,再在Rt△AOB中,根据三角函数求出OB=AB•sin60°,即可求出BD=2OB=6$\sqrt{3}$.
解答 解:如图所示: ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,OB=$\frac{1}{2}$BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=6cm,∠BAO=60°,
在Rt△AOB中,OB=AB•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴BD=2OB=6$\sqrt{3}$.
点评 本题考查了菱形的性质、等边三角形的判定与性质以及三角函数的运用;熟练掌握菱形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
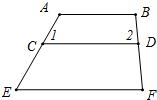 如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.
如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论. 如图,在△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠C=34°,求∠DAE的大小.
如图,在△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠C=34°,求∠DAE的大小.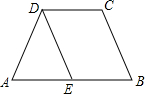 如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC
如图,在四边形ABCD中,∠A=∠B,∠C=∠ADC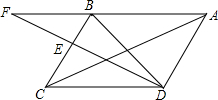 已知:如图,在菱形ABCD中,E为边BC的中点,DE与对角线AC交于点F,若∠BAC=∠EDC且EF=1,DF=2,则AC的长为2.
已知:如图,在菱形ABCD中,E为边BC的中点,DE与对角线AC交于点F,若∠BAC=∠EDC且EF=1,DF=2,则AC的长为2.