题目内容
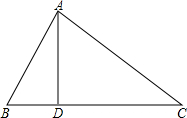 如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长.
如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长.考点:勾股定理,等腰三角形的判定与性质
专题:
分析:作∠DAC的平分线交BC于点E,作EF⊥AC于点F.易证△ADB≌△ADE≌△AFE,然后根据全等三角形的对应边相等推知BD=DE=EF=3,AD=AF,设AD=AF=y,则在Rt△ACD中,利用勾股定理即可求得AD的长度,进而可得出AB的长.
解答: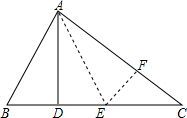 解:作∠DAC的平分线交BC于点E,作EF⊥AC于点F.则∠BAD=∠DAE=∠EAF.
解:作∠DAC的平分线交BC于点E,作EF⊥AC于点F.则∠BAD=∠DAE=∠EAF.
∵∠CAD=2∠BAD,
∴∠BAD=∠EAD,
在△ADB与△ADE中,
,
∴△ADB≌△ADE(ASA).
同理可得,△ADB≌△ADE≌△AFE,
∴BD=DE=EF=3,AD=AF.
∵EC=CD-DE=5,
∴FC=
=4,
设AD=AF=y,则在Rt△ACD中,x2+82=(x+4)2,
解得,x=6,
∴AD=6,
∴AB=
=
=3
.
 解:作∠DAC的平分线交BC于点E,作EF⊥AC于点F.则∠BAD=∠DAE=∠EAF.
解:作∠DAC的平分线交BC于点E,作EF⊥AC于点F.则∠BAD=∠DAE=∠EAF.∵∠CAD=2∠BAD,
∴∠BAD=∠EAD,
在△ADB与△ADE中,
|
∴△ADB≌△ADE(ASA).
同理可得,△ADB≌△ADE≌△AFE,
∴BD=DE=EF=3,AD=AF.
∵EC=CD-DE=5,
∴FC=
| 52-32 |
设AD=AF=y,则在Rt△ACD中,x2+82=(x+4)2,
解得,x=6,
∴AD=6,
∴AB=
| AD2+BD2 |
| 62+32 |
| 5 |
点评:本题考查了勾股定理、全等三角形的判定与性质.注意,勾股定理应用的前提条件是在直角三角形中.

练习册系列答案
相关题目
 已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.
已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.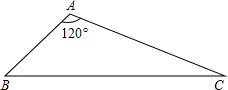 如图,AB=2,AC=4,∠BAC=120°,求BC及S△ABC.
如图,AB=2,AC=4,∠BAC=120°,求BC及S△ABC. 如图,?ABCD中,∠C=108°,BE平分∠ABC,交AD于E,求∠BED的度数.
如图,?ABCD中,∠C=108°,BE平分∠ABC,交AD于E,求∠BED的度数. 如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径. 如图,要把边长为6的正三角形剪成一个最大的正六边形,
如图,要把边长为6的正三角形剪成一个最大的正六边形, 如图,在△ABC中,中位线EF与中线AD相交于点O.求证:AD与EF互相平分.
如图,在△ABC中,中位线EF与中线AD相交于点O.求证:AD与EF互相平分.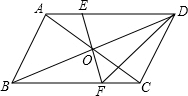 如图,AC、BD为?ABCD的对角线,O为两条对角线的交点,过点O作EF⊥BD,与AD、BC分别交于点E、F,试猜想DE与DF之间的关系,并说明理由.
如图,AC、BD为?ABCD的对角线,O为两条对角线的交点,过点O作EF⊥BD,与AD、BC分别交于点E、F,试猜想DE与DF之间的关系,并说明理由. 如图,已知:OE、OF分别是AB、AC的垂直平分线,∠OBC、∠OCB的平分线交于点P,求证:OP⊥BC.
如图,已知:OE、OF分别是AB、AC的垂直平分线,∠OBC、∠OCB的平分线交于点P,求证:OP⊥BC.