题目内容
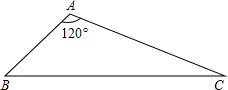 如图,AB=2,AC=4,∠BAC=120°,求BC及S△ABC.
如图,AB=2,AC=4,∠BAC=120°,求BC及S△ABC.考点:勾股定理,含30度角的直角三角形
专题:
分析:延长BA,过点C作CD⊥BA交于点D,首先根据邻补角互补计算出∠DAC=60°,再计算出∠ACD=30°,根据直角三角形的性质可得AD=
AC=2,然后利用勾股定理计算CD长,再计算出BC长,最后利用△BDC的面积减去△ADC的面积可得S△ABC.
| 1 |
| 2 |
解答: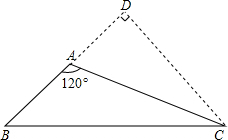 解:延长BA,过点C作CD⊥BA交于点D,
解:延长BA,过点C作CD⊥BA交于点D,
∵∠BAC=120°,
∴∠DAC=60°,
∴∠ACD=30°,
∵AC=4,
∴AD=2,
∴BD=4,CD=
=
=2
,
∴BC=
=
=2
,
S△ABC=S△BDC-S△ACD=
×4×2
-
×2×2
=4
-2
=2
.
 解:延长BA,过点C作CD⊥BA交于点D,
解:延长BA,过点C作CD⊥BA交于点D,∵∠BAC=120°,
∴∠DAC=60°,
∴∠ACD=30°,
∵AC=4,
∴AD=2,
∴BD=4,CD=
| AC2-AD2 |
| 16-4 |
| 3 |
∴BC=
| DB2+CD2 |
| 16+12 |
| 7 |
S△ABC=S△BDC-S△ACD=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
点评:此题主要考查了勾股定理,关键是正确作出辅助线,掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
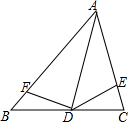 如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC.
如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC. 如图,在六边形ABCDEF中,所有角都相等.
如图,在六边形ABCDEF中,所有角都相等.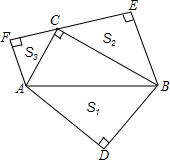 如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.
如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3. 如图所示,若∠3=∠1+∠2,试猜想AB与CD之间关系?
如图所示,若∠3=∠1+∠2,试猜想AB与CD之间关系?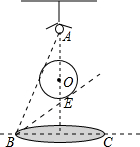 如图,有一悬挂的球,球心为点O,球正上方A处有一小灯泡,球在桌面上投下的阴影是一个圆,其直径BC=30cm,在B处看球,最大仰角是60°,最小仰角是30°,求球心O到桌面的距离.
如图,有一悬挂的球,球心为点O,球正上方A处有一小灯泡,球在桌面上投下的阴影是一个圆,其直径BC=30cm,在B处看球,最大仰角是60°,最小仰角是30°,求球心O到桌面的距离. 如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试画出一个三角形使边长为3
如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试画出一个三角形使边长为3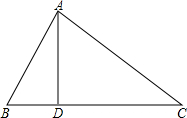 如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长.
如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长.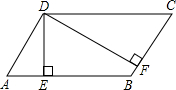 如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,DE:DF=2:3,?ABCD的周长是50,求?ABCD各边的长.
如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,DE:DF=2:3,?ABCD的周长是50,求?ABCD各边的长.