题目内容
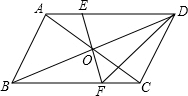 如图,AC、BD为?ABCD的对角线,O为两条对角线的交点,过点O作EF⊥BD,与AD、BC分别交于点E、F,试猜想DE与DF之间的关系,并说明理由.
如图,AC、BD为?ABCD的对角线,O为两条对角线的交点,过点O作EF⊥BD,与AD、BC分别交于点E、F,试猜想DE与DF之间的关系,并说明理由.考点:平行四边形的性质
专题:
分析:首先根据平行四边形的性质可得DO=BO,AD∥FB,然后再证明△DEO≌△BFO,可得EO=FO,再由条件EF⊥BD可得DO是EF的垂直平分线,根据线段垂直平分线的性质可得ED=DF.
解答:解:DE=DF,
∵四边形ABCD是平行四边形,
∴DO=BO,AD∥FB,
∴∠EDB=∠FBD,
在△DEO和△BFO中,
,
∴△DEO≌△BFO(ASA),
∴EO=FO,
∵EF⊥BD,
∴DE=DF.
∵四边形ABCD是平行四边形,
∴DO=BO,AD∥FB,
∴∠EDB=∠FBD,
在△DEO和△BFO中,
|
∴△DEO≌△BFO(ASA),
∴EO=FO,
∵EF⊥BD,
∴DE=DF.
点评:此题主要考查了平行四边形的性质,关键是掌握平行四边形对角线互相平分,对边平行.

练习册系列答案
相关题目
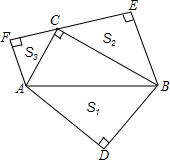 如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.
如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.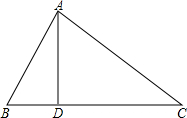 如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长.
如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长. 如图是几个小正方体搭的几何体的俯视图,画出这个几何体的主视图和左视图,并在每一个小正方形内标出行列所对应方块的个数.
如图是几个小正方体搭的几何体的俯视图,画出这个几何体的主视图和左视图,并在每一个小正方形内标出行列所对应方块的个数.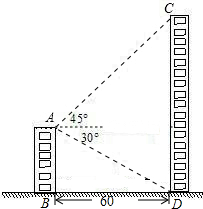 如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字).
如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字). 如图,点F在直线AB上,已知∠1和∠D互余,CF⊥DF.求证:AB∥CD.
如图,点F在直线AB上,已知∠1和∠D互余,CF⊥DF.求证:AB∥CD.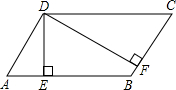 如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,DE:DF=2:3,?ABCD的周长是50,求?ABCD各边的长.
如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,DE:DF=2:3,?ABCD的周长是50,求?ABCD各边的长.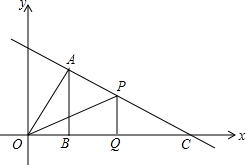 如图,一次函数y=-
如图,一次函数y=- 如图,如果半径为1个单位长度的圆上有一点A,且点A与数轴上表示5.1的点重合(圆与数轴只有这一个交点),让圆沿数轴的负方向滚动一周,点A到达另一点B,则A,B两点之间表示整数的点共有( )
如图,如果半径为1个单位长度的圆上有一点A,且点A与数轴上表示5.1的点重合(圆与数轴只有这一个交点),让圆沿数轴的负方向滚动一周,点A到达另一点B,则A,B两点之间表示整数的点共有( )