题目内容
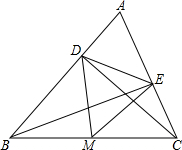 已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.
已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.(1)若DE=3,BC=8,求△DME的周长;
(2)若∠A=60°,求证:∠DME=60°;
(3)若BC2=2DE2,求∠A的度数.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:
分析:(1)根据直角三角形斜边上中线性质求出DM=
BC=4,EM=
BC=4,即可求出答案;
(2)根据三角形内角和定理求出∠ABC+∠ACB=120°,根据直角三角形斜边上中线性质求出DM=BM,EM=CM,推出∠ABC=∠BDM,∠ACB=∠CEM,根据三角形内角和定理求出即可;
(3)求出EM=
EN,解直角三角形求出∠EMD度数,根据三角形的内角和定理求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据三角形内角和定理求出∠ABC+∠ACB=120°,根据直角三角形斜边上中线性质求出DM=BM,EM=CM,推出∠ABC=∠BDM,∠ACB=∠CEM,根据三角形内角和定理求出即可;
(3)求出EM=
| 2 |
解答:解:(1)∵CD,BE分别是AB,AC边上的高,
∴∠BDC=∠BEC=90°,
∵M是线段BC的中点,BC=8,
∴DM=
BC=4,EM=
BC=4,
∴△DME的周长是DE+EM+DM=3+4+4=11;
(2)证明:∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵∠BDC=∠BEC=90°,M是线段BC的中点,
∴DM=BM,EM=CM,
∴∠ABC=∠BDM,∠ACB=∠CEM,
∴∠EMC+∠DMB=180°-120°=60°,
∴∠DME=180°-120°=60°;
(3)解: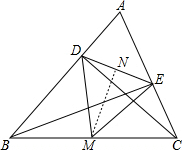 过M作MN⊥DE于N,
过M作MN⊥DE于N,
∵DM=EM,
∴EN=DN=
DE,∠ENM=90°,
∵EM=DM=
BC,DN=EN=
DE,BC2=2DE2,
∴(2EM)2=2(2EN)2,
∴EM=
EN,
∴sin∠EMN=
=
,
∴∠EMN=45°,
同理∠DMN=45°,
∴∠DME=90°,
∴∠DMB+∠EMC=180°-90°=90°,
∵∠ABC=∠BDM,∠ACB=∠CEM,
∴∠ABC+∠ACB=
(180°-∠DMB+180°-∠EMC)=135°,
∴∠BAC=180°-(∠ABC+∠ACB)=45°.
∴∠BDC=∠BEC=90°,
∵M是线段BC的中点,BC=8,
∴DM=
| 1 |
| 2 |
| 1 |
| 2 |
∴△DME的周长是DE+EM+DM=3+4+4=11;
(2)证明:∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵∠BDC=∠BEC=90°,M是线段BC的中点,
∴DM=BM,EM=CM,
∴∠ABC=∠BDM,∠ACB=∠CEM,
∴∠EMC+∠DMB=180°-120°=60°,
∴∠DME=180°-120°=60°;
(3)解:
 过M作MN⊥DE于N,
过M作MN⊥DE于N,∵DM=EM,
∴EN=DN=
| 1 |
| 2 |
∵EM=DM=
| 1 |
| 2 |
| 1 |
| 2 |
∴(2EM)2=2(2EN)2,
∴EM=
| 2 |
∴sin∠EMN=
| EN |
| EM |
| ||
| 2 |
∴∠EMN=45°,
同理∠DMN=45°,
∴∠DME=90°,
∴∠DMB+∠EMC=180°-90°=90°,
∵∠ABC=∠BDM,∠ACB=∠CEM,
∴∠ABC+∠ACB=
| 1 |
| 2 |
∴∠BAC=180°-(∠ABC+∠ACB)=45°.
点评:本题考查了等腰三角形的判定和性质,三角形的内角和定理,解直角三角形的性质,直角三角形斜边上中线性质的应用,能综合运用性质进行推理是解此题的关键,本题综合性比较强,有一定的难度,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
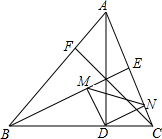 如图,锐角△ABC中,AD,BE,CF是三条高,DM⊥BE于M,DN⊥CF于N
如图,锐角△ABC中,AD,BE,CF是三条高,DM⊥BE于M,DN⊥CF于N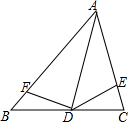 如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC.
如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC.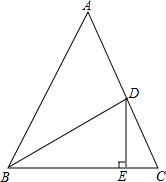 已知△ABC中,BD平分∠ABC,DE⊥BC于E点,且DE:BD=1:2,DC:AD=3:4,CE=
已知△ABC中,BD平分∠ABC,DE⊥BC于E点,且DE:BD=1:2,DC:AD=3:4,CE= 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于 为了适应车流量的增加,想把桥洞改为双行道,并且要使宽为1.2米,高为2.8米的卡车能安全通过,那么此桥洞的宽至少应增加多少米?
为了适应车流量的增加,想把桥洞改为双行道,并且要使宽为1.2米,高为2.8米的卡车能安全通过,那么此桥洞的宽至少应增加多少米? 如图,在六边形ABCDEF中,所有角都相等.
如图,在六边形ABCDEF中,所有角都相等.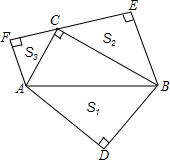 如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.
如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.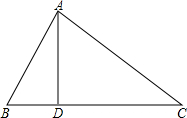 如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长.
如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长.