题目内容
 如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.考点:垂径定理,勾股定理
专题:
分析:过点O作OD⊥AB于点D,连接OA,先根据垂径定理得出AD的长,再由勾股定理求出OD的长,进而可得出结论.
解答: 解:过点O作OD⊥AB于点D,连接OA,
解:过点O作OD⊥AB于点D,连接OA,
∵PA=AB=2,PO=5,
∴AD=1,
∴PD=PA+AD=2+1=3,
∴OD=
=
=4,
∴OA=
=
=
.
答:⊙O的半径是
.
 解:过点O作OD⊥AB于点D,连接OA,
解:过点O作OD⊥AB于点D,连接OA,∵PA=AB=2,PO=5,
∴AD=1,
∴PD=PA+AD=2+1=3,
∴OD=
| OP2-PD2 |
| 52-32 |
∴OA=
| AD2+OD2 |
| 12+42 |
| 17 |
答:⊙O的半径是
| 17 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于 如图所示,若∠3=∠1+∠2,试猜想AB与CD之间关系?
如图所示,若∠3=∠1+∠2,试猜想AB与CD之间关系? 如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试画出一个三角形使边长为3
如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试画出一个三角形使边长为3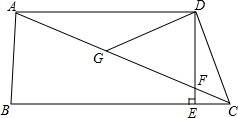 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.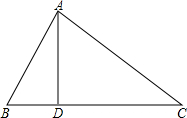 如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长.
如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,若BD=3,CD=8.求AB的长. 如图,点C在线段AB上,点M、N分别是AC,BC的中点.
如图,点C在线段AB上,点M、N分别是AC,BC的中点.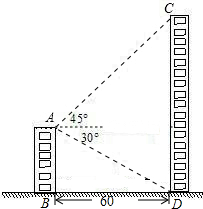 如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字).
如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字).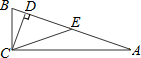 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点.求∠ECD的度数.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点.求∠ECD的度数.