题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象开口向下,并经过点(-1,2),(1,0),下列命题其中一定正确的是 ;(把你认为正确结论的序号都填上)
①当x≥0时,函数值y随x的增大而增大;
②当x≤0时,函数值y随x的增大而减小;
③存在一个正数m,使得当x≤m时,函数值y随x的增大而增大;当x≥m时,函数值y随x的增大而减小;
④存在一个负数m,使得当x≤m时,函数值y随x的增大而增大;当x≥m时,函数值y随x的增大而减小;
⑤a+2b>-2c.
①当x≥0时,函数值y随x的增大而增大;
②当x≤0时,函数值y随x的增大而减小;
③存在一个正数m,使得当x≤m时,函数值y随x的增大而增大;当x≥m时,函数值y随x的增大而减小;
④存在一个负数m,使得当x≤m时,函数值y随x的增大而增大;当x≥m时,函数值y随x的增大而减小;
⑤a+2b>-2c.
考点:二次函数的性质
专题:
分析:根据二次函数的对称性判断出对称轴在y轴左侧,然后根据二次函数的增减性判断出①、②错误;然后对③④作出判断,再根据二次函数图象上点的坐标特征求出a+b+c=0,然后乘2表示出a+2b+2c,再根据a是负数整理即可判断出⑤正确.
解答:解:∵二次函数y=ax2+bx+c(a≠0)的图象开口向下,并经过点(-1,2),(1,0),
∴二次函数与x轴的另一个交点在x=-1的左边,
∴对称轴在y轴的左侧,
∴当x≥0时,函数值y随x的增大而减小,故①错误;
当x≤0时,函数值y随先x的增大而增大,然后随x的增大而减小,故②错误;
存在一个负数m,使得当x≤m时,函数值y随x的增大而增大;当x≥m时,函数值y随x的增大而减小,故③错误,④正确;
∵抛物线经过点(1,0),
∴a+b+c=0,
∴2a+2b+2c=0,
∴a+2b+2c=-a>0,
∴a+2b>-2c,故⑤正确,
综上所述,命题正确的是④⑤.
故答案为:④⑤.
∴二次函数与x轴的另一个交点在x=-1的左边,
∴对称轴在y轴的左侧,
∴当x≥0时,函数值y随x的增大而减小,故①错误;
当x≤0时,函数值y随先x的增大而增大,然后随x的增大而减小,故②错误;
存在一个负数m,使得当x≤m时,函数值y随x的增大而增大;当x≥m时,函数值y随x的增大而减小,故③错误,④正确;
∵抛物线经过点(1,0),
∴a+b+c=0,
∴2a+2b+2c=0,
∴a+2b+2c=-a>0,
∴a+2b>-2c,故⑤正确,
综上所述,命题正确的是④⑤.
故答案为:④⑤.
点评:本题考查了二次函数的性质,主要利用了二次函数的增减性和对称性,二次函数图象上点的坐标特征,难点在于⑤把所得等式扩大2倍并表示出-a.

练习册系列答案
相关题目
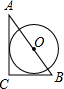 已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )
已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在①AB=CD;②AD=CB;③EF分别是AB、CD的中点;④DE=BF这四个命题,选取三个作为条件,能否得出下列结论,并说明理由.
如图,在①AB=CD;②AD=CB;③EF分别是AB、CD的中点;④DE=BF这四个命题,选取三个作为条件,能否得出下列结论,并说明理由.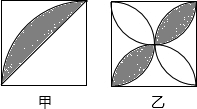 如图(甲)、(乙)是两个边长相等的正方形,甲图以边为半径在正方形内画圆弧,连接对角线;乙图以各边为直径在正方形内画半圆,阴影部分的面积分别记为S甲、S乙,那么S甲和S乙的大小关系是:S甲
如图(甲)、(乙)是两个边长相等的正方形,甲图以边为半径在正方形内画圆弧,连接对角线;乙图以各边为直径在正方形内画半圆,阴影部分的面积分别记为S甲、S乙,那么S甲和S乙的大小关系是:S甲 如图,等腰直角△ABC中,∠BAC=90°,AB=AC,点M、N在边BC上,且∠MAN=45°,MB=1,CN=3,求MN的长.
如图,等腰直角△ABC中,∠BAC=90°,AB=AC,点M、N在边BC上,且∠MAN=45°,MB=1,CN=3,求MN的长.