题目内容
20.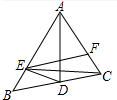 如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.
如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.(1)求证:△AED≌△ACD;
(2)点F为AC上一点,连接EF、EC,若EC平分∠DEF,试说明∠AED与∠EFC满足怎样的数量关系.
分析 (1)根据SAS即可判定△AED≌△ACD.
(2)结论:∠AED+∠EFC=180°,只要证明:EF∥BC得∠EFC+∠ACD=180°,由此即可证明.
解答 (1)证明: ∵AD是△ABC平分线,
∵AD是△ABC平分线,
∴∠DAE=∠DAC,
在△ADE和△ADC中,
$\left\{\begin{array}{l}{AD=AD}\\{∠DAE=∠DAC}\\{AE=AC}\end{array}\right.$,
∴△AED≌△ACD.
(2)结论:∠AED+∠EFC=180°,理由如下,
解:∵△AED≌△ACD,
∴∠AED=∠ACD,DE=DC,
∴∠DEC=∠ECD,
∵∠DEC=∠CEF,
∴∠DE=∠FEC,
∴EF∥BC,
∴∠EFC+∠ACD=180°,
∴∠AED+∠EFC=180°.
点评 本题考查全等三角形的判定和性质、平行线的判定和性质,解题关键是利用全等三角形解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
 如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )| A. | x<2 | B. | x>2 | C. | x>1 | D. | x<1 |
 观察如图,每个小正方形的边长均为1.
观察如图,每个小正方形的边长均为1. 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB=8,AD=10,那么EC=3.
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB=8,AD=10,那么EC=3.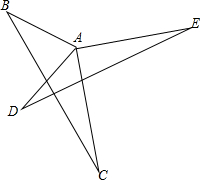 如图,已知AB=AD,AC=AE,∠DAB=90°,∠EAC=90°.说明:
如图,已知AB=AD,AC=AE,∠DAB=90°,∠EAC=90°.说明: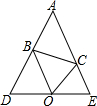 已知:△ABC中,∠ABC与∠ACB外角平分线交于点O,过O作直线交AB,AC延长线于点D,E,且AD=AE.求证:
已知:△ABC中,∠ABC与∠ACB外角平分线交于点O,过O作直线交AB,AC延长线于点D,E,且AD=AE.求证: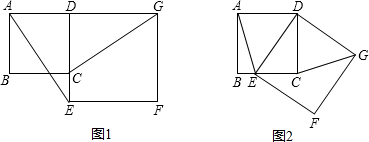
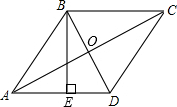 如图,已知菱形对角线BD、AC的长分别为12cm和16cm,求菱形的高BE.
如图,已知菱形对角线BD、AC的长分别为12cm和16cm,求菱形的高BE.