题目内容
7. 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB=8,AD=10,那么EC=3.
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB=8,AD=10,那么EC=3.
分析 先根据矩形的性质得AD=BC=10,AB=CD=8,再根据折叠的性质得AF=AD=10,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC-BF=4,设CE=x,则DE=EF=8-x,然后在Rt△ECF中根据勾股定理得到x2+42=(8-x)2,再解方程即可得到CE的长.
解答 解:∵四边形ABCD为矩形,
∴AD=BC=10,AB=CD=8,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=10,EF=DE,
在Rt△ABF中,∵BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=6,
∴CF=BC-BF=10-6=4,
设CE=x,则DE=EF=8-x
在Rt△ECF中,∵CE2+FC2=EF2,
∴x2+42=(8-x)2,解得x=3.
故答案是:3.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.

练习册系列答案
相关题目
1.五一期间,囊阳旅行社组织198人到古隆中和鹿门寺旅游,到古隆中的人数比到鹿门寺的人数2倍少3人,若设到古隆中旅游的人数为x人,到鹿门寺旅游的人数为y人,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{x=2y-3}\\{x+y=198}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2y=x-3}\\{x+y=198}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2(y-3)}\\{x+y=198}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2(y+3)}\\{x+y=198}\end{array}\right.$ |
 如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s).
如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s).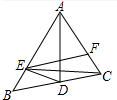 如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.
如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.