题目内容
12.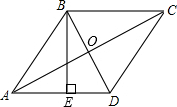 如图,已知菱形对角线BD、AC的长分别为12cm和16cm,求菱形的高BE.
如图,已知菱形对角线BD、AC的长分别为12cm和16cm,求菱形的高BE.
分析 根据菱形的对角线互相垂直平分,利用勾股定理求出菱形的边长,再根据菱形的面积等于对角线乘积的一半和底乘以高的两种求法即可求解.
解答  解:如图,∵菱形ABCD中,对角线BD=12cm,AC=16cm,
解:如图,∵菱形ABCD中,对角线BD=12cm,AC=16cm,
∴OA=$\frac{1}{2}$AC=8cm,OD=$\frac{1}{2}$BD=6cm,AC⊥BD,
∴AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=10cm,
设菱形的高BE=hcm,
则菱形的面积=$\frac{1}{2}$AC•BD=AD•BE,
∴$\frac{1}{2}$×16×12=10h,
解得h=9.6.
故菱形的高BE为9.6cm.
点评 本题主要考查菱形的对角线互相垂直平分的性质,面积等于两对角线乘积的一半和底乘以高的两种求法,利用勾股定理求出菱形的边长是解题的关键.

练习册系列答案
相关题目
1.五一期间,囊阳旅行社组织198人到古隆中和鹿门寺旅游,到古隆中的人数比到鹿门寺的人数2倍少3人,若设到古隆中旅游的人数为x人,到鹿门寺旅游的人数为y人,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{x=2y-3}\\{x+y=198}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2y=x-3}\\{x+y=198}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2(y-3)}\\{x+y=198}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2(y+3)}\\{x+y=198}\end{array}\right.$ |
 如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s).
如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s).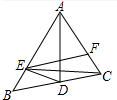 如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.
如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.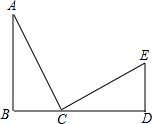 如图,已知:AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,证明:AC⊥CE.
如图,已知:AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,证明:AC⊥CE.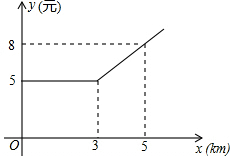 某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.