题目内容
5.如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC,易证△DAE≌△DCG,可得结论:①AE=CG;②AE⊥CG.如图2,将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,连接AE和CG,你认为图1中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.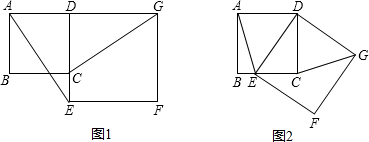
分析 延长AE和GC相交于点H,根据正方形的性质可得AD=DC,DE=DG,∠ADC=∠DCB=∠B=∠BAD=∠EDG=90°,再根据同角的余角相等求出∠1=∠2,然后利用“边角边”证明△ADE和△CDG全等,根据全等三角形对应角相等可得∠5=∠4,再根据平角等于180°求出∠6=∠7,然后求出∠EHC=90°,再根据垂直的定义证明即可.
解答 证明:延长AE和GC相交于点H,
∵在正方形ABCD与正方形DEFG中,AD=DC,DE=DG,
∠ADC=∠DCB=∠B=∠BAD=∠EDG=90°,
∴∠1=∠2=90°-∠3,
在△ADE与△CDG中,$\left\{\begin{array}{l}{AD=CD}\\{∠1=∠2}\\{DE=DG}\end{array}\right.$,
∴△ADE≌△CDG,
∴∠5=∠4,AE=CG,
又∵∠5+∠6=90°,
∴∠4+∠7=180°-∠DCE=180°-90°=90°,∠6=∠7,
又∵∠6+∠AEB=90°,∠AEB=∠CEH,
∴∠CEH+∠7=90°,
∴∠EHC=90°,
∴AE⊥GC;
点评 本题考查了正方形的性质,全等三角形的判定与性质,垂直的定义,熟记性质并确定出全等的三角形是解题的关键,利用阿拉伯数字表示角更形象直观.

练习册系列答案
相关题目
15.某种蔬菜按品质分成三个等级销售,销售情况如表:
则售出蔬菜的平均单价为44元/千克.
| 等级 | 单价(元/千克) | 销售量(千克) |
| 一等 | 50 | 20 |
| 二等 | 45 | 40 |
| 三等 | 40 | 40 |
 已知,如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF,
已知,如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF,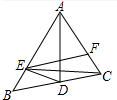 如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.
如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.