题目内容
15.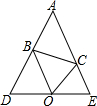 已知:△ABC中,∠ABC与∠ACB外角平分线交于点O,过O作直线交AB,AC延长线于点D,E,且AD=AE.求证:
已知:△ABC中,∠ABC与∠ACB外角平分线交于点O,过O作直线交AB,AC延长线于点D,E,且AD=AE.求证:(1)DO=OE;
(2)△BDO∽△OEC.
分析 (1)欲证明DO=OE只要证明△OMD≌△ONE即可.
(2)先证明∠D=90°-$\frac{1}{2}$∠A,∠BOC=90°-$\frac{1}{2}$∠A,所以∠BOC=∠D,由∠BOE=∠BOC+∠COE=∠D+∠DBO得∠COE=∠DBO,由此即可证明.
解答 (1)证明:作OM⊥AD,ON⊥AE,OF⊥BC垂足分别为M、N、F.
∵OB平分∠CBD,OC平分∠BCE,
∴OM=OF=ON,
∵AD=AE,
∴∠D=∠E,
在△ODM和△OEN中,
$\left\{\begin{array}{l}{∠D=∠E}\\{∠OMD=∠ONE}\\{OM=ON}\end{array}\right.$,
∴△OMD≌△ONE,
∴OD=OE.
(2)∵∠BOC=180°-(∠OBC+∠OCB)=180°-$\frac{1}{2}$(∠DBC+∠ECB)=180°-$\frac{1}{2}$(∠A+∠ACB+∠A+∠ABC)=90°-$\frac{1}{2}$∠A,
$∠D=\frac{1}{2}(180°-∠A)$=90°-$\frac{1}{2}$∠A,
∴∠BOC=∠D,
∵∠BOE=∠BOC+∠COE=∠D+∠DBO,
∴∠COE=∠DBO,
∵∠D=∠E,
∴△BDO∽△OEC.
点评 本题考查全等三角形的判定和性质、角平分线的性质、利用角平分线的性质添加辅助线是解决问题的关键,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s).
如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s).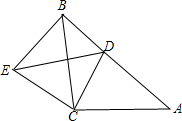 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.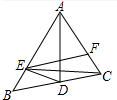 如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.
如图,AD是△ABC平分线,点E在AB上,且AE=AC,连接ED.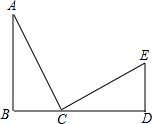 如图,已知:AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,证明:AC⊥CE.
如图,已知:AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,证明:AC⊥CE.